2015-07-14
345
Доказательство ведём индукцией по числу вершин Р в дереве редукций.
Базис Р =1.
+ С помощью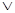 
избавляемся от многосукцедентности.
v •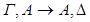 
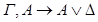
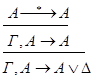
что и требовалось.
Пусть утверждение справедливо для Р<k, докажем для P=k.
Рассмотрим все возможные случаи (6 штук):
1) редукция & - справа.
+ • 
+ • 
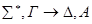
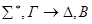
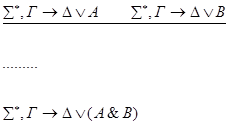
+• v
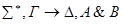
По индукционному предположению доказаны секвенции, соответствующие дочерним вершинам.
Построим доказательство секвенции, соответствующей v. Для этого достаточно доказать секвенцию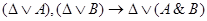 
, и затем применить 2 раза правило сечения.
2) редукция &- слева.
+ •
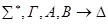
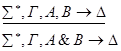
+ • v
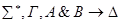
По индукционному предположению доказана секвенция, приписанная дочерней вершине. Построим доказательство секвенции, приписанной v. Она доказуема по правилу удаления &.
3) редукция v- справа.
+ •
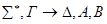
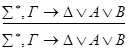тривиально
+ • v
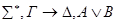
4) редукция v – слева.
• •
+ +
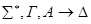
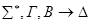
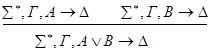
+• v
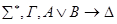
По индукционному предположению доказываются секвенции, приписанные дочерним вершинам. Построим доказательство секвенции, приписанной v. Она доказывается по правилу удаления .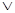
5) редукция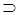 
– слева.
• •
+ +
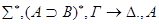
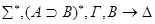
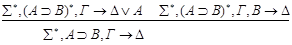
+• v
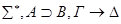
По индукционному предположению доказываются секвенции, приписанные дочерним вершинам. Построим доказательство секвенции, приписанной v: .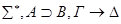
Аналогично п.1 докажем сначала секвенцию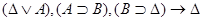 
,
и применим затем 2 раза правило сечения.
6) редукция 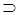– справа (2 рода).
+
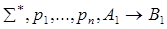
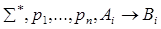
+ v
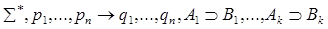
По индукционному предположению доказывается одна из секвенций, приписанных дочерним вершинам. Построим доказательство секвенции, приписанной v: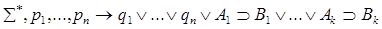 
.
Доказательство состоит в применении правила введения 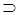и правил введения V.
Утверждение 1 доказано.
