Доказательство

1. По дереву редукций построим минимальное отрицательное дерево D*.

Берём корневую вершину дерева редукций, она помечена «-», включаем её в поддерево.

Если к ней применялась редукция 1-го рода, то одну из дочерних вершин, помеченную «-», тоже включаем в поддерево. Если к ней применялась редукция 2 рода, то в минимальное дерево включаем все дочерние вершины, помеченные «-».

И т.д. Поступаем аналогично со всеми внутренними вершинами дерева редукций, пока не дойдём до листьев, помеченных «-».

Т.о. построим минимальное, отрицательное дерево D*.

2. По дереву D* построим интерпретацию Крипке Kр=<W, w₀, R, 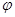> следующим образом.

1). W. Миры – это участки редукции 1 рода, которые оканчиваются на вершинах, к которым приписаны секвенции вида 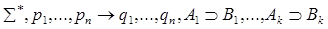. Они формируют множество возможных миров W={w₀, w₁,…}.

Т.е. с каждым миром ассоциируется вершина с приписанной секвенцией .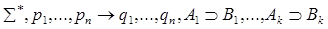

2) w₀ – мир, в который входит корневая секвенция.

3). R. Отношение достижимости. R(u, v)определяется так: R(u, v) – истинно, если в минимальном отрицательном дереве D* существует путь, проходящий из u в v.

Отметим, что если некоторая вершина-лист u помечена значком <-,w>, то мы будем считать что из u имеется путь в w.

Очевидно, что так определенное отношение достижимости удовлетворяет свойствам рефлексивности и транзитивности.

4) 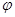. В каждом мире определим значения элементарных высказываний.

- v

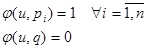
- •u для всех остальных переменных q.

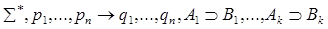
Пропозициональные переменные, один раз попав в антецедент секвенции, исчезнуть не могут, т.к. входят в антецеденты всех «верхних» секвенций. Поэтому свойство монотонности разметки очевидно выполняется: если любая пропозициональная переменная истина в мире u, то она истина во всех мирах, достижимых из него.

Докажем, что формула F принимает 0 в реальном мире w₀.

Доказательство проведём индукцией по сложности Р = <N, M> формулы G, входящей в секвенцию, приписанную вершине v в минимальном отрицательном дереве D*. Здесь N – число логических связок в формуле G, а M–количество вершин, расположенных над v в дереве D*.

Отношение порядка. Пусть P1 = <N1,M1> и P2 = <N2,M2>.

Тогда P1 < P2 т. и т.т. когда N1 < N2 или N1 =N2 & M1<M2.

Так определенное отношение обладает свойством фундированности (следовательно, по нему можно вести индукцию).

Индукционное предположение: «Пусть v -вершина дерева D*, принадлежащая к миру w, и G – формула сложности P, входящая в 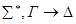- секвенцию, приписанную v. Тогда если G – формула из 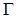, то она истинна в w, а если G – формула из 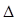, то она ложна в w».

a) Базис. P= <0, 0>.

–•v

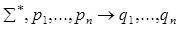Ни одну редукцию применить нельзя.

По построению интерпретации Кр все переменные 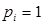в w, и все переменные

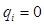в w.

б) Пусть для всех формул сложности Р < <N,M> утверждение справедливо. Докажем, что оно справедливо и для формул со сложностью Р = <N,M>,

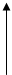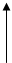w { – • v 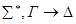Докажем, что φ(w,Г)=1

φ(w,Δ)=0

Рассмотрим все возможные случаи (6 штук):

1)

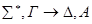
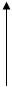
– • u

– •v

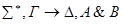
К формулам из u применяем индукционное предположение (сложность меньше Р).

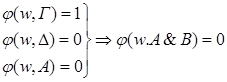
2)

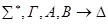
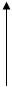
– • u

– •v

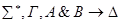
К формулам из u применяем индукционное предположение (сложность меньше Р).

3)

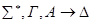
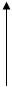
– • u

– •v

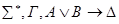
К формулам из u применяем индукционное предположение (сложность меньше Р).

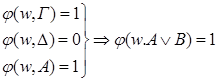
4)

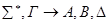
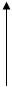
– • u

– •v

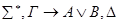
К формулам из u применяем индукционное предположение (сложность меньше Р).

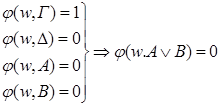
5а)

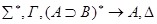
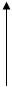
– • u

– •v

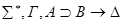
К формулам из u применяем индукционное предположение (сложность меньше Р).

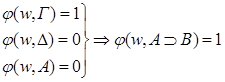
Во всех мирах, достижимых из данного либо А=0, либо В=1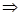

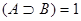
5б)

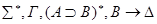
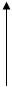
– • u

– •v

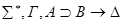
К формулам из u применяем индукционное предположение (сложность меньше Р).

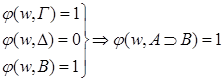
6а)

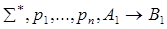
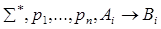
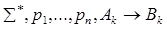
– w1 –wi

- w

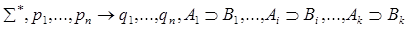
Согласно индукционному предположению в w_i:

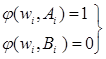
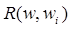: w_i достижим из w по построению R.

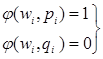по определению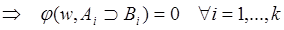

либо А=1, либо В=0

6б) вершина w помечена значком <-, u> и ей приписана секвенция

.

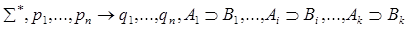По индукционному предположению 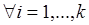, найдется мир v достижимый из u, в котором

.

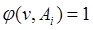
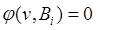Отсюда следует, что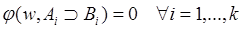

Утверждение 2 доказано.

Теорема о полноте полностью доказана.