Вопросы и задания для самостоятельной работы 4 страница

частного верно. Здесь возможен, например, такой диалог учителя с учеником,
Уч и т ел ь: Угадай, чему равно частное 20 и 10?
У ч е н и к: Мне, кажется, частное равно 2.
У ч и т е л ь: Как убедиться в правильности твоей догадки?
У ч е н и к: Нужно выполнить проверку с помощью умножения.
У ч и т ел ь: Как делается проверка?
У ч е н и к: Частное умножается на делитель. Если получится делимое, частное угадано правильно; 2 умножить на 10— получим 20. Значит, 20: 10 равно двум.
Аналогично выполняются и другие упражнения типа 22:11, 30:15, 24:12 и т. д.
В случаях, когда угадать значение частного трудно, ученикам предлагается находить его подбором, перебирая однозначные числа по порядку, начиная, например, с двух. Когда у учащихся будет накоплен опыт, методика подбора может быть усовершенствована. Подбор например, можно начинать с числа 5, а затем, в зависимости от результата умножения 5 на делитель, следующее пробное число выбирать большим или меньшим 5. Например, при делении 98 на 14 предполагают, что частное равно.5:14•5=7О, значит, число 5 мало, нужно пробовать число 6:14.6=84—получено число меньше делимого, значит и б мало для значения частного. Пробуется число 7:14.7=98. Таким образом, 98:14=7.
Можно подсказать учащимся, что при подборе значения частного
следует обращать внимание на последние цифры делимого и делите- -
ля. Так как делимое оканчивается цифрой 8, а делитель — цифрой 4,
то достаточно вспомнить, какое число нужно умножить на 4, чтобы
произведение оканчивалось цифрой 8. Таких чисел два — 2 и 7.
Число 2 не подходит, так как слишком мало. Значит, частное равно 7.
Выполняется проверка.
Наиболее полно результаты изучения темы деления двузначного числа на двузначное могут быть использованы при обучении учащихся письменному делению. А оно изучается в концентре Многозначные числа. Поэтому, вероятно, деление на двузначные числа целесообразнее изучать непосредственно перед темой Деление многозначных чисел>.
Деление с остатком. Эта тема используется при изучении алгоритма письменного деления. Изучая деление, необходимо рассмотреть с учащимися и случаи, когда одно число не делится на другое нацело. Тему Деление с остатком целесообразно изучать в два приема. В теме внетабличные случаи деления можно показать учащимся, что значит разделить с остатком, некоторые свойства такого деления. Компоненты при этом подбираются таким образом, чтобы для деления было достаточно знания табличных случаев (например, 25:4, 38:6, 71:8 и т. д.).
Обратиться к теме деления с остатком в самом начале изучения операции деления важно еще и потому, что деление с остатком встречается в реальной жизни значительно чаще, чем удобное табличное деление.
Вначале рассматриваются задачи такого содержания: У мальчика 20 к. Сколько тетрадей по цене З к. он сможет купить за эти деньги?»; «В коробке 25 конфет. Их разделили поровну между б детьми. Сколько конфет получил каждый из них?»; ‘В классе 35 учеников. Сколько парт должно быть в этом классе?» и т. д.

При решении задач используются наглядные средства. Например, первая из задач может быть проиллюстрирована с помощью кружков (однокопеечных монет) (рис. 29). I1ллюстраиия не только позво

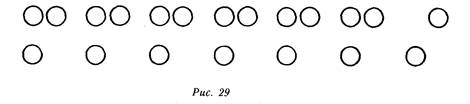
ляет решить задачу, но и ввести понятие «остаток». Практическое решение задачи математизируется: 20:3 = б (ост. 2). В результате решения еще нескольких подобных задач учащиеся могут прийти к выводу, что для получения ответа совсем не обязательно представлять содержание задачи в наглядной форме.

Приведем фрагмент урока, на котором учитель подводит учащихся к «открытию» приема деления с остатком.

Таким образом, учащиеся приходят к выводу: чтобы число разделить на данное число (с остатком), нужно взять самое большое число, делящееся на делитель, но меньше делимого. Не обязательно заучивать это правило наизусть. Важно, чтобы ученики умели применять его на практике. В качестве тренировочных упражнений полезно рассмотреть такую систему частных, которая позволяет учащимся увидеть закономерность,, связывающую делитель и остаток:

У ч и т е л ь: Итак рассмотренная задача решается выражением 25:4 (рассматривалась, например, одна из задач, приведенных выше). Табличное ли это деление?

Ученик: Нет.

У ч и т е л ь: Сколько единиц нужно взять из 25, чтобы они целиком разделились на 4?

Уч е н и к: Например, 4, 8, 12, 16, 20, 24.

У ч и т е л ь: Если мы возьмем и разделим 4 единицы, то сколько единиц останется разделить?

Ученик: 21.

У ч и т е л ь: Сколько единиц можно взять из этого числа, чтобы они разде. лились на 4?

Ученик: Или 4, или 8, или 16, или 20.

У ч и т е л ь: А сколько единиц можно было бы взять из 25 для деления на 4, чтобы не делить на единицы по частям?

У ч е н и к: 24 единицы.

У ч и т е л ь: Чему равнялось бы частное?

У ч е н и к: б и одна единица осталась бы.

У ч и т е л ь: Если бы пришлось делить 37 на 4, то сколько единиц из этого числа нужно было бы сразу взять, чтобы получить самый маленький остаток?

У ч е н и к: Из всех чисел, которые делятся на 4, нужно было бы взять самое большое число, но чтобы оно было меньше 37. Это число 36.

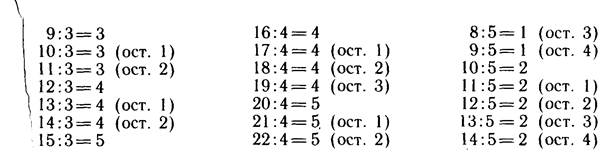
Анализ результатов деления позволяет сделать вывод, что остаток при делении не может быть больше делителя (при условии, что максимальное число единиц делимого разделено на делитель).

Возможно, конечно, что кто-нибудь из учащихся получит «парадоксальный» ответ: 45:7= 5 (ост. 10). Чтобы помочь ему заметить ошибку, нужно обратить его внимание на то, все ли единицы делимостью разделены? 10 можно делить на 7, значит, частное подобрано неверно. Правильный ответ: частное 6, остаток 3.

16. ТЫСЯЧА

Общие положения. Известно, что наряду с концентрами «десяток» и «Сотня» в начальном курсе математики выделяется концентр «Тысяча». Это объясняется тем, что при изучении трехзначных чисел учащиеся усваивают качественно новые сведения из области нумерации чисел и очень важные алгоритмы выполнения арифметических операций.

Изучая нумерацию трехзначных чисел, ученики знакомятся с новым разрядом — сотен. Тем самым завершается формирование класса единиц. Это позволяет в дальнейшем делать более крупные шаги в изучении нумерации: числа, большие тысячи, будут вводиться не по разрядам, а по классам.

При изучении концентра «Тысяча» расширяются знания учащихся об операциях сложения и вычитания. Они усваивают приемы письменного сложения и вычитания, которые впоследствии используются и на множестве многозначных чисел.

Нумерация и сравнение чисел. При изучении нумерации чисел в пределах десяти естественными наглядными пособиями были множества реальных предметов, более абстрактные множества палочек, геометрических фигур. Изучение нумерации в пределах ста потребовало более сложных пособий, например, таких, как абак. Однако для того чтобы изобразить, например, число 500, потребовался бы абак с 50 карманами. Поэтому при изучении нумерации сложения и вычитания в пределах тысячи используется позиционный абак. Особенность его состоит в том, что наглядный материал, изображающий единицы, десятки и сотни, имеет один и тот же вид это или косточки счетов, или квадраты, или палочки. Зато карманы абака — их всего три — выполняют разные функции. Палочка, находящаяся в крайнем левом кармане (рис. 30), означает единицу. Если палочку положить в средний карман, она будет означать десяток, а если в крайний правый,—.- то сотню. Заметим, что принцип изображения чисел на непозиционном абаке был другим: карманам не приписывалось

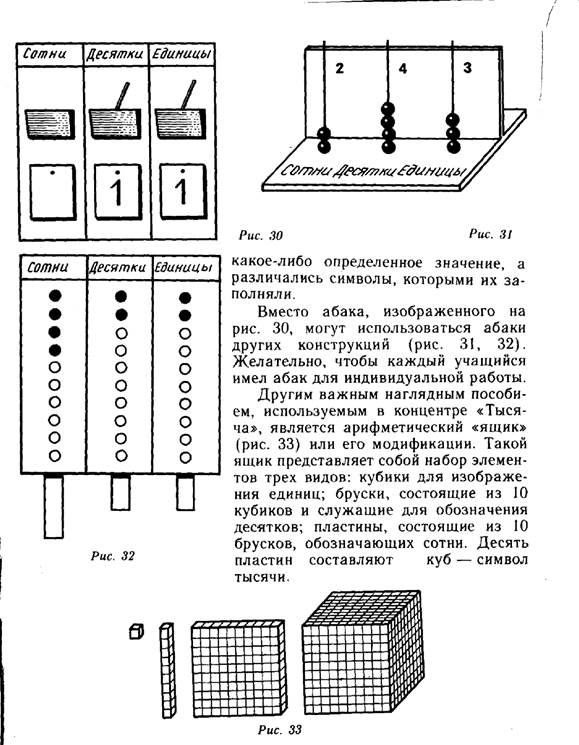
для демонстраций у доски и индивидуальной работы удобен более простой вариант арифметического «ящика». Роль единиц играют квадраты, десятков полоски, состоящие из 10 квадратов. Большие Квадраты,* состоящие из 10 полосок или 100 маленьких квадратов, служат для изображения сотен. Эти материалы могут быть изготовлены из плотной бумаги или картона.

Нумерация чисел от 10 до 100 изучалась в три приема: нумерация
4 чисел второго десятка, круглых десятков, остальных двузначных чи4ел Это объяснялось тем, что образование названий чисел второго
,десятка, круглых десятков и остальных двузначных чисел имеет
особенности.
Названия трехзначных чисел образуются либо из названия круглы сотен, либо из названия круглых сотен и двузначных или однозначны чисел в сочетании. Поэтому знакомство учащихся с нумерации трехзначных чисел осуществляется в два приема. Сначала
школьники учатся называть и записывать трехзначные числа,
оканчивающиеся нулями, а потом остальные трехзначные
чи сл а.
Кр уг л ы е сот н и. Сущность методики знакомства учащихся ‘
числами этого вида состоит, во-первых, в том, чтобы показать им,
что считать сотнями можно так же, как единицами и десятками, и что
любое число сотен в пределах десяти имеет особое название.
Вначале учащиеся подсчитывают количество квадратов, укладываемы по одному в наборное полотно: «Один, два девять».
Затем в наборное полотно по одной укладываются полоски
(«десятки»). По мере заполнения полотна учащиеся считают: «Один
десяток квадратов, два десятка квадратов девять десятков квадратов» Обращается внимание, что количество квадратов можно называют по-другому: «десять квадратов, двадцать девяносто
квадратов».
Рассматривается модель новой счетной единицы — больший
квадрат (пластинка), состоящий из 10 полосок. Так как каждая
полоска содержит 10 квадратов-единиц, то констатируется, что пластинка содержит 100 таких квадратов. Поэтому, когда в наборное
полотно пластинки укладываются по одной, школьники считают: «0д-
на сотня квадратов, две сотни квадратов девять сотен квадратов».
Учитель говорит, что- число квадратов в каждом из этих случаев
можно назвать: сто, двести девятьсот. Обращается внимание
учащихся на особенности и сходство в названиях сотен: две-сти,
три-ста, четыре-ста, пять-сот девять-сот.
Одновременно с названием круглых сотен выполняются операции
сложения и вычитания: 5 еот.+3 сот.=8 сот., 7 сот.—2 сот.=
= 5 сот. и т. д. С помощью наглядных пособий учащиеся учатся
отвечать на вопросы: «Сколько десятков в сотне,..., какое число
соответствует 20 десяткам, 50 десяткам, б сотням?» и т. д.
Устная нумерация трехзначных чисел. Параллельно
с заучиванием учащимися названий круглых сотен начинается работ над устной нумерацией остальных трехзначных чисел. Это связан с тем, что при счете сотнями у учащихся может сложиться
впечатление, что за числом сто, например, непосредственно следует
двести, за двести - триста и т. д. Появление названий трехзначных чисел происходит «естественно», при выполнении учениками
упражнений такого вида: «Назови число квадратов, изображенных
на наборном полотне» (рис. 34). Учащиеся отвечают: «сто и двадцать три», «триста и сорок», «двести и пять». Предлагается

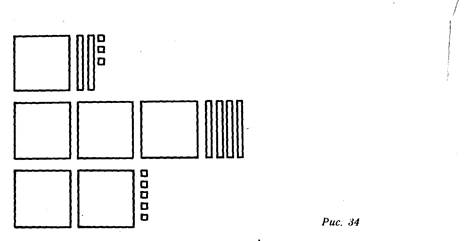
называть число квадратов без использования союза «и»: сто двадцать три, триста сорок и т. д.

Затем предлагаются более сложные упражнения: необходимо назвать число, состоящее из 2 сотен и 5 единиц; 7 сотен и 8 десятков; 9 сотен, 2 десятков и б единиц и т. д. По возможности эти упражнения выполняются без использования наглядных пособий.

Одновременно учащимся предлагаются упражнения другого рода. Они отвечают на вопросы: «Сколько сотен, единиц и десятков содержится в числах пятьсот сорок три, двести шестьдесят один, шестьсот два, сто семьдесят?»

Они также должны выполнять разнообразные упражнения.

Назови по порядку числа от девяносто семи до ста четырех, от ста девяносто девяти до двухсот трех и т. д.

Назови число, следующее за числом триста девяносто девять; число, меньшее на единицу, чем пятьсот; большее на два, чем восемьсот девяносто девять, и т. д.

Назови числа, которые находятся между числом триста двадцать шесть и триста тридцать один, и т. д.

для работы над этими упражнениями используются модели числового луча — числовая лента, рулетка.

Письменная нумерация трехзначных чисел. Работа над устной нумерацией проводится с опорой на арифметический ящик (его модификации). При изучении письменной нумерации используется позиционный абак. Прежде чем приступить к изучению записи трехзначных чисел, учащиеся учатся изображать на абаке число элементов некоторого множества, и наоборот, определять число элементов множеств по изображению на абаке. В качестве множеств могут использоваться множества квадратов, представленных отдельными квадратами, полосками и пластинками.

Обучение работе с абаком сводится к формированию у учащихся достаточно простого алгоритма. В абаке есть спицы. Крайняя справа предназначена для изображения количества единиц, т. е. отдельных квадратов. На нее нанизывается столько косточек, сколько отдельных квадратов изображено. На вторую спицу нанизываются косточки, которые показывают, сколько полосок (десятков), содержит данное число. Наконец на третью

спицу косточки, соответствующие

сотням (пластинкам) данного числа.

Все эти пояснения следуют по ходу изображения числа (квадратов) на абаке.

Например, на абаке нужно отложить число 567. для наглядности

его можно представить в виде множества квадратов (пластинок, полосок и отдельных квадратов). Затем, в соответствии с числом единиц (квадратов), десятков (полосок), сотен (пластинок), заполняются спицы абака (рис. 35).

В дальнейшем при выполнении подобных упражнений («Изобразите на абаке число») можно не представлять число в наглядном виде.

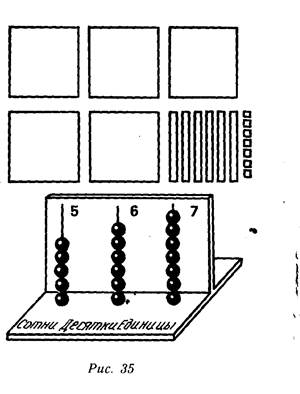
Полезны упражнения и другого вида: назвать число, изображенное на абаке. Операции рассмотренного алгоритма выполняются в обратном порядке: сначала подсчитывается количество косточек на спице сотен и называется число сотен в числе, затем - количество косточек на спице десятков и называется число десятков и т. п. Рядом с соответствующими спицами абака записываются цифры.

Учащимся предлагается записывать в тетради цифры, соответствующие показаниям абака, в таком же порядке (слева направо),

в каком расположены на абаке спицы сотен, десятков и единиц.

Каждую цифру пишут ‘в отдельную клетку тетради. Так появляются

записи: 667, 445 и т. д. Трехзначные числа на первых порах читаются

с опорой на абак.

Поясним последнее на примере. На доске записывается число 327. Требуется объяснить, что означает эта запись.

У ч и тел ь: Что означает цифра 3?

У ч е н и к: Это означает, что на спице сотен три косточки.

У ч и т е л ь: Что показывают эти косточки?

Учен и к: В числе З сотни.

У ч и тел ь: Что означает цифра 2?

Уч и тел ь: Какое же число записано на доске?

Уче н и к: Триста двадцать семь.

С помощью абака рассматривается запись трехзначных чисел особого вида: 200, 209, 290, 400, 470, 407, 500, 505 и т. п. При необходимости снова можно использовать арифметический «ящик».

Например, ставится задача изобразить на абаке и записать число двести. В этом числе 2 сотни, значит, на спице сотен абака откладываются две косточки. Нужно ли откладывать косточки на спице десятков? Очевидно, что нет, так как свободных десятков в числе двести нет. Все они заключены в двух сотнях — двадцать полосок объединены в две пластинки. Такое объяснение позволяет избежать неверной формулировки: <в числе двести нет десятков. Аналогично объясняется отсутствие единиц в разряде единиц числа

200. В соответствии с иллюстрацией на абаке записывается число 200.

В дальнейшем, когда учащиеся смогут записывать и читать трехзначные числа без опоры на абак, они учатся представлять такие числа в виде суммы разрядных слагаемых.

Из концентра «Сотня известно, как на языке математики записывается, что число 46, например, состоит из 4 десятков и б единиц:

46=40+6. Этот способ обобщается для трехзначных чисел: число

256 состоит из 2 сотен, 5 десятков и б единиц, поэтому 256= =200+50+6. Рассматриваются и более сложные случаи: 206= 200+6, 250=200+50 и т. д. Одновременно изучаются и случаи вычитания, основанные на знании разрядного состава трехзначного числа:842—2=840,842—4О=8О2,842—8ОО=42,57О__7О5у 570—500=70, 409 —9=400, 409—400=9 и т. д.

При выполнении упражнений такого рода учащиеся, с одной стороны, закрепляют знание разрядного состава и поместного значения цифр в трехзначном числе, с другой,— готовятся к изучению операций сложения и вычитания на множестве трехзначных чисел.

Важную роль в изучении нумерации трехзначных чисел играют составные именованные числа, выраженные в мерах длины, стоимости. Использование таких чисел возможно на любом этапе знакомства учащихся с позиционным принципом нумерации. В частности, использование мер длины может помочь учащимся представлять некоторые трехзначные числа в виде двузначных именованных чисел. Такой прием в дальнейшем используется для вычисления значения сумм и разностей определенного вида. Например, чтобы показать, что число 490 содержит 49 десятков и может быть представлено в виде 49 десятков, рассматривается следующая система упражнений: «Сколько дециметров содержится в 4 м и 9 дм? в 490 см? в 590 см?> и т. д.

Сравнение чисел в пределах 1 000 осуществляется аналогично сравнению чисел в пределах 100. Прежде всего необходимо установить, что всякое трехзначное число, даже самое маленькое, больше любого, даже самого большого, двузначного числа (100 99). Этим самым сравнение чисел в пределах 1000 сводится к сравнению трехзначных чисел.

На примерах выясняется, что из двух трехзначных чисел то

больше, у которого цифра сотен больше (321 285, 505 з 396 и т. п.). Если же цифры сотен двух сравниваемых чисел равны, то сравниваются цифры десятков, и то число больше, у которого цифра десятков больше (485 478, 315з 308 и т. п.). Если же и цифры десятков равны, то сравниваются цифры единиц, и то число больше, у которого цифра единиц больше (576 572, 105 101 и т. п.).

два трехзначных числа равны тогда и только тогда, когда цифры и одноименных разрядов (сотен, десятков, единиц) равны (одинаковы).

Описанный алгоритм можно представить (для учителя, конечно) в виде схемы (рис. 36). Пусть необходимо сравнить два трехзначных числа: А1 = х1с11е и А2 = с2сi2е2, где с!, й, е1 —

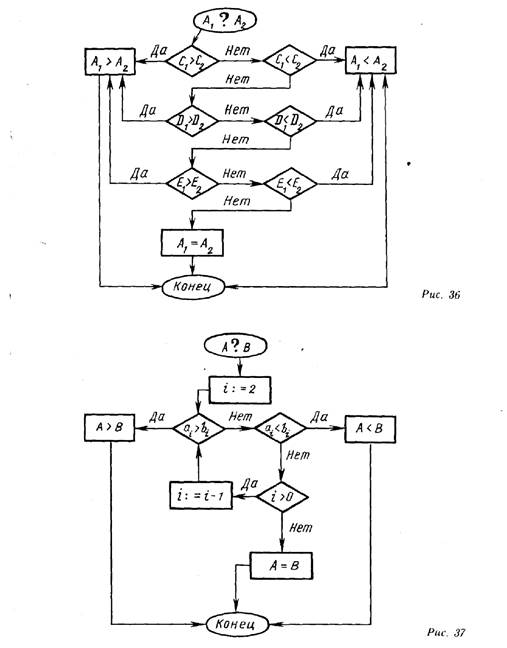
цифры сотен, десятков и единиц числа А1, а с2, i2, е2.— цифры сотен, десятков и единиц числа А2.

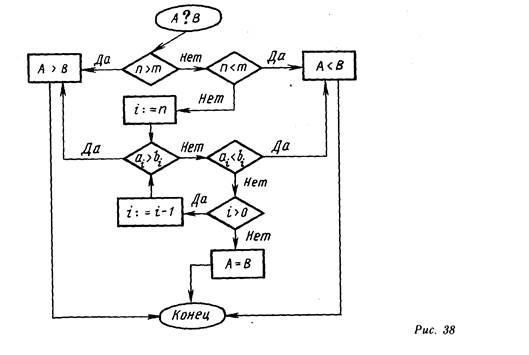
Однако эта схема алгоритма построена нерационально, хотя по дидактическим соображениям более понятна. Циклический характер процесса сравнения отражается в более простой схеме (рис. 37). Введем следующие обозначения: А и В — сравниваемые числа А = а2аiао, В = Ь1Ь2Ь0. Этот алгоритм легко обобщается для сравнения двух многозначных чисел: А В =... Ь1Ь0 (рис. 38).

Сложение и вычитание (устные вычисления). В концентре «Тысяча» учащиеся овладевают принципиально новыми умениями— письменного сложения и вычитания чисел. Вместе с тем раскрываются широкие возможности для упражнения школьников в устном счете в новых условиях — на множестве трехзначных чисел. Учитель должен Использовать эти возможности. Это, во-первых, позволяет закрепить навыки устного счета, которые учащиеся приобрели в концентре «Сотня». Во-вторых, такой счет полезен при усвоении нумерации Трехзна4ных чисел, принципа позиционного счисления. В-третьих, у учеников вырабатывается привычка обращаться к письменным вычислениям лишь тогда, когда ВЫПОЛНИТЬ вычисления устно трудно.

Выделяют две группы сумм и разностей, значения которых учащиеся должны уметь вычислять устно.

К первой группе относятся суммы и разности, значения которых определяются в буквальном смысле слова без вычислений. Для этого используется знание разрядного состава чисел, позиционного принципа записи чисел. Эти суммы и разности имеют вид: 400+2, 400+ 20, 400+ 25, 405+ 20, 450+ 2, 420—.-20, 420—400, 402—2, 402 — 400, 425 — 5, 425 — 20, 425 — 400. Значения подобных выражений вычисляются еще в период учащимися нумерации трехзначных чисел. Затруднения в такого рода вычислениях свидетельствуют о том, что ученик плохо усвоил нумерацию. В этих случаях необходимо обратиться к помощи абака.

Вторая группа включает следующие выражения: 70+50,1 120—70, 560+240, 560—240, 670+ 190, 670—190 и т. д. Их значения определяются на основе знания учащимися табличных случаев сложения и вычитания или приемов устного сложей1ВБТЯiВТЯ в пределах ста. Однако эти знания нельзя применить к данным выражениям непосредственно. Выражения приводятся к удобному виду с помощью уже известного приема замены двузначного числа однозначным именованным числом. Рассмотрим использование этого

приема на конкретных примерах:

500 — 300

5 сот.—З сот.=2 сот.

500—300= 200

таблица сложения и вычитания;

240 + 380

24 дес.+38 дес.=62 дес.

240+380= 620

620 — 380

62 дес.—38 дес.=24 дес.

620—380= 240

Здесь используются приемы устного сложения и вычитания.

Суммы и разности такого вида мо>но рассматривать сразу после усвоения нумерации трехзначных чисел.

Умножение и деление (устные вычисления). Прием сведения новых случаев сложения и вычитания к ранее изученным может быть использован и для некоторых случаев умножения и деления в пределах тысячи. Так, произведения и частные вида 200. 3, 600:3, 70.5, 350:7 можно представить как 2 сот.:3, б сот.:3, 7 дес. 5, 35 лес.:7. Для их вычисления достаточно знать таблицу умножения и соответствующие случаи деления.

Произведения и частные вида 120.3, 240.2, 170.5 и 360:3, 720:8, 560:7 с помощью того же приема представляют как произведения и частные двузначных и однозначных чисел. Для их вычисления используются приемы устного умножения и деления.

Письменные приемы (сложения и вычитания). Алгоритмы сложения и вычитания в столбик, усвоенные учащимися в начальных классах, используются на протяжении всех лет обучения математике в средней школе. Качество усвоения этих алгоритмов в значительной степени зависит от того, насколько ясно они представлены ученикам. Важную роль при этом играют средства наглядности и главным образом позиционный абак.

500 + 300

5 сот.+3 сот.=8 сот.

500+300= 800

Здесь используется

80 + 90

8 дес.+9 дес.=17 дес.

80+90= 170

170—90

17 дес.—9 дес.=8 дес.

170—90= 80

Определим последовательность и методику изучения различных

ВИДОВ сумм в порядке Возрастающей СЛОЖНОСТИ.

‘_- Сначала рассматриваются самые простые случаи: 256+300,

256+40, 256+1. Нахождение ЭТИХ сумм Легко Иллюстрируется с

Помощью абака. К уже имеющимся на абаке КОСТОЧКАМ показывающим Первое слагаемое 256, Последовательно присоединяют

З КОСТОЧКИ на СПИЦУ СОТЕН, ИЛИ 4 КОСТОЧКИ на спицу Десятков, или одну на спицу единиц. Затем ЭТИ случаи обобщаются - к числу

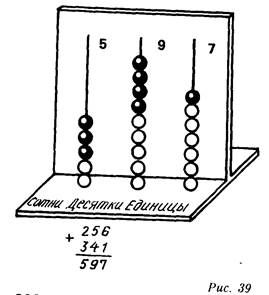
256 прибавляется 341. Манипуляции с абаком (рис. 39) описываются

математически

256+З41 (200+ЗОО)+ (50+40) + (б+I)==5ОО+9О+7=597

Очевидно, Правило прибавления суммы к сумме МОЖНО было бы ввести через задачи. С помощью Системы Целесообразных задач

задач

можно было бы также Показать, ЧТО этим правилом в некоторых случаях удобно Пользоваться для Вычислений И, наконец, МОЖНО было бы Побудить учащихся ЗАПОМНИТЬ формулировку этого Правила. Однако все ЭТО Оказывается ИЗЛИШНИМ, если Использовать абак. С его помощью прием Письменного сложения МОЖНО представить очень наглядно

действия, выполненные на

абаке, Записываются и по-другому — столбиком (см. РИС. 39). Аналогичная Запись появляется на тетрадях учащихся. Запись в тетрадях учитель сопровождает объяснением, как следуетподпц1..

объяснением, как следуетподпц1.. одно слагаемое Под другим: числа б и 1 записываются СТРОГО одно под Другим, Потому что б Косточек и одна нанизаны на одну и ту же спицу абака. Поясняется, почему цифра 4 подписывается ПОД цифрой 5, а З - ПОД цифрой 2, зачем ПРОВОДИТСЯ горизонтальная Черта - она Отделяет Слагаемые от значения Суммы, Где Ставится знак действия. Сложение в столбик гораздо удобнее и нагляднее, чем сложение в строчку.

Навыки записи Слагаемых и значения Суммы в столбик закрепляются при вычислении сумм аналогичного вида (сумма единиц одноименного разряда слагаемых меньше 10).

Следующим ПО СЛОЖНОСТИ ВИДОМ сумм является сумма, в Которой При сложении единиц какого-либо разряда - Образуется единица старшего Разряда: 354+236, 354+237, 354+452, 354+462.

Учащимся следует напомнить, ЧТО при сложении однозначных Чисел, Например 5 и 8, получается Двузначное число, т. е. образуется единица старшего разряда - разряда Десятков, Эта единица записывается на соответствующем месте. Ученики знают также, как найти сумму, например, чисел 25 и 8. При сложении 5 и 8 также получается новый десяток, который приплюсовывается к уже имеющимся двум десяткам. Все ЭТО позволяет упростить объяснение приема вычисления сумм нового вида. И все же на первых порах не стоит запрещать учащимся записывать промежуточные результаты сложения. Необходимо также побуждать учащихся использовать индивидуальные абаки. На демонстрационном абаке (рис. 40, а) изображается, например, сложение чисел 354 и 236. По ходу

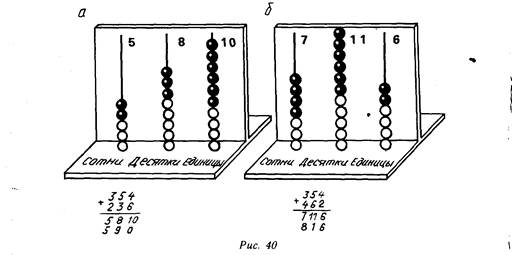
работы с абаком учитель дает следующие пояснения: «На спице единиц оказалось 10 косточек, т. е. десяток. Но десяток изображается на абаке одной косточкой на спице десятков. Значит, к тем косточкам, которые, находятся на спице десятков—их 8, нанизываем еще одну косточку, а со спицы единиц все косточки снимаем.

Для нескольких примеров такого рода учащиеся могут делать подробную запись, фиксируя промежуточную сумму (рис. 40,а). Выполняемые операции комментируются ими, например, следующим образом: «К б прибавить 4, получится 10. В разряде единиц записываю ноль, а один десяток запоминаю. К 5 прибавить 3, получится 8, и еще один десяток — получится 9. В разряде десятков записываю

9. К З сотням прибавить 2, Получится 5 сотен. В разряде сотен записываю 5. Ответ 590.

В дальнейшем они проговаривают промежуточные операции более кратко: «К 4 прибавить 6—10, 0 пишу, 1 запоминаю. К 5 прибавить 3—8, и еще один — 9. К З прибавить 2—5. Сумма равна 590».

Вычисление сумм вида 354 + 237 несущественно отличается от рассмотренных выше.

При вычислении сумм, в которых при сложении десятков образуется сотня, полезно обратиться к абаку. Так же как и в предыдущем случае, несколько примеров можно выполнить с записью промежуточной суммы (рис. 40, 6).

Наконец, рассматривается самый сложный случай сложения трехзначных чисел, когда при сложении разрядных единиц образуется и десяток и сотня: 354 +246, 354 +267 и т. д.

Сначала сложение выполняется на абаке (рис. 41, а). Последовательно объясняется замена 10 единиц десятком (рис. 41, 6), а

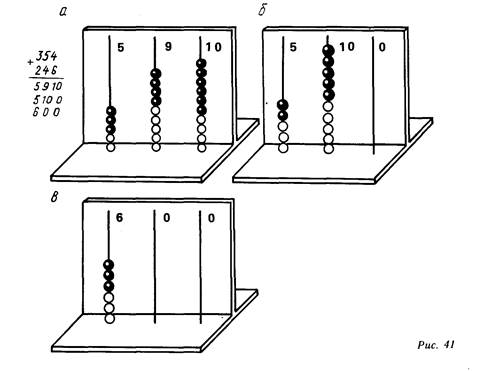
затем 10 десятков—сотней (рис. 41, в). В записи действия в столбик каждая из ситуаций, представленных на абаке (рис. 41), фиксируется в виде промежуточной суммы. Эти записи подробно комментируются.

После детального рассмотрения еще одного-двух примеров промежуточные суммы не записываются, а запоминаются. При необходимости учащиеся дают краткие пояснения. Например, для случая

354+267: «к 4 прибавить 7—! 1. Один пишу, один запоминаю. к 5 прибавить 6—1 1 и еще один 12, два пишу, один запоминаю. К З прибавить 2—5 и еще 1—6. Сумма равна 621».

В процессе закрепления приема сложения в столбик будут встречаться и другие «особые» случаи, например 295+405, 585+ 15,308+407 и т. д. Не исключено, что в некоторых из этих случаев ученикам снова придется обратиться к абаку.

В заключение учитель на конкретном примере объясняет, почему сложение в столбик начинается с единиц младшего разряда.

Если начать складывать числа 367 и 594 с разряда сотен, то в сумму придется дважды вносить поправки: 367

+ 594

Если же начать сложение с единиц, этого можно избежать.

При изучении приема письменного вычитания, так же как и при сложении, последовательно рассматриваются разные по сложности случаи.

Самый простой случай, например 382—261, 427—225, учащиеся в основном могут объяснить самостоятельно. действия иллюстрируются с помощью абака и записываются на математическом

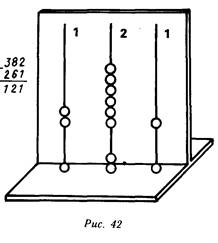языке (рис. 42):

382—261 =(300—200)+

+ (80—60) + (2— 1) = 100 +

+20+1 = 121.

(Знакомить учащихся с какими-

либо новыми «правилами» сложения

и вычитания нет необходимости. Операции, выполняемые на абаке, естественны, и смысл их очевиден.)

По аналогии со сложением в столбик видно, что записывать операцию вычитания экономнее столбиком. Учащиеся, вероятно, способны объяснить, как записывается вычитаемое под уменьшаемым. Вычитание, подобно сложению, начинается с разряда единиц.

Рассматриваются более сложные случаи вычитания, когда в одном из разрядов уменьшаемого меньше единиц, чем в соответствующем разряде вычитаемого: 382—263, 382—291 и т. д. Объяснить особенность вычислений в этих случаях можно проще, если связать их с уже изученным приемом сложения в столбик с образованием дополнительных разрядных единиц.