2015-07-14
505
Поиск считается результативным, если выявлена хотя бы одна ситуация несовпадения бит атрибута и ячейки накопителя.
| А | F≠ | |||||||
| М | ||||||||
| F1 | F2 | F3 | F4 |
Если для j-го разрядного среза данных F≠ij=1, то для всех остальных разрезов i-й ячейки памяти значение поисковой функции будет равно 1 (не зависимо от дальнейшего сопоставления – “бегущая единица”).
| А | F≠ | |||||||
| М | ||||||||
| F0 = 0 | ||||||||
| 0 | ||||||||
| F1 | F2 | F3 | F4 |
При поиске на несовпадение, если старший бит маски М1 = 0, следует, что F1 = F0 =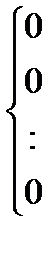 
|
|
|
Выполним формальный синтез ячейки накопителя для операций поиска F= и F≠. Опишем работу ячейки накопителя в виде таблицы истинности.
| Яij Qij |
| Ai |
| Mij |
| Fij-1 |
| Fij |
| Ai |
| Mij |
Представим ячейку накопителя как черный ящик, у которого имеются три входа (Fi,j-1, Ai, M1i), один выход (Fi,j), внутреннее состояние (бит данных Qij).
Опишем работу ячейки в виде таблицы:
| M1j | F=ij-1 | Ai | Qij | F=ij | |
| т. к. М1i = 0; то Fij = Fij-1 | |||||
| т. к. Fij-1 = 0 (“бегущий ноль”) | |||||
| Fij = Я(М1i, Fi-1,j, Ai, Qij) | |||||
Рис.11
Получим аналитическую запись функции с помощью карты Карно:
Рис.12
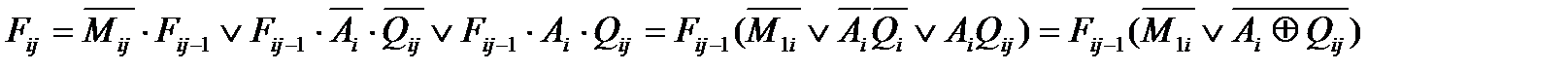Построим таблицу истинности для операции поиска на несовпадение:
| M1j | F≠ij-1 | Ai | Qij | F≠ij | |
| т. к. М1i = 0; то Fij = Fij-1 | |||||
| т. к. F≠ij-1 = 1 (“бегущая единица”) | |||||
Рис.13
|
|
|
На основе таблицы истинности получим аналитическую запись функции:
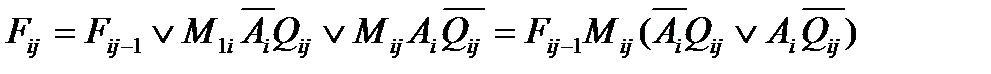
Пример.
| А | F= | |||||||
| М1 | ||||||||
| F0 | F1 | F2 | F3 | F4 | ||||
| А | F= | |||||||
| М1 | ||||||||
| F0 | F1 | F2 | F3 | F4 |
ЛЕКЦИЯ 7,8.
