Метод векторных диаграмм

Гармонические колебания (1.7) допускают наглядную графическую интерпретацию. Ее смысл состоит в том, что каждому гармоническому колебанию с частотой 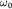можно поставить в соответствие вращающийся с угловой скоростью 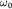вектор, длина которого равна амплитуде 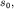а его начальное (стартовое) положение задается углом 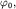совпадающим с начальной фазой (рис. 1.5).

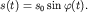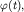Вертикальная проекция вектора изменяется со временем: Мгновенное положение вектора определяется углом который называется фазой и равен: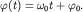

При угловой скорости (круговой частоте) 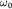вектор совершает 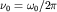оборотов (циклов) в секунду, а продолжительность одного оборота (период) равна отношению угла 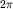к угловой скорости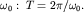

С помощью векторных диаграмм легко осуществить сложение гармонических колебаний. Так, если необходимо сложить два гармонических колебания с одинаковыми частотами

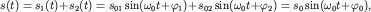
то амплитуду 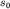и начальную фазу 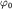суммарного колебания 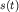с той же частотой 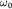можно легко рассчитать из рис. 1.6а, на котором графически изображена операция сложения векторов 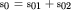в момент времени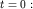

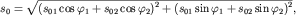
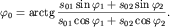
Ясно, что вертикальная проекция вектора будет также изменяться по гармоническому закону с частотой 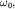поскольку взаимное расположение векторов 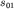и 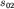не изменяется с течением времени.