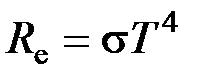2015-07-14
475
, где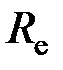 
- излучательность абсолютно черного тела; 
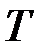- термодинамическая температура; 
- постоянная Стефана-Больцмана.
Излучательность серого тела
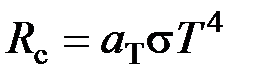, где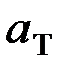 
- коэффициент черноты (коэффициент излучения) серого тела.
Закон смещения Вина
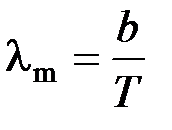, где 
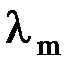- длина волны, на которую приходится максимум энергии излучения; 
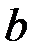- постоянная закона смещения Вина.
Зависимость максимальной спектральной плотности излучательности от температуры
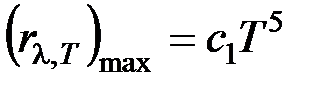, где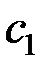 
- постоянная в законе, связывающем максимальную спектральную плотность энергетической светимости черного тела с термодинамической температурой.
Формула Эйнштейна для фотоэффекта
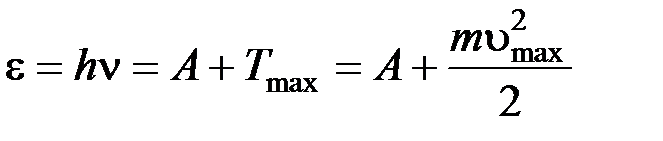, где 
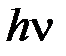- энергия фотона, падающего на поверхность металла; 
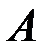- работа выхода электрона; 
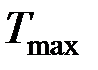- максимальная кинетическая энергия фотоэлектрона; 
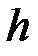- постоянная Планка.
В случае, если энергия фотона много больше работы выхода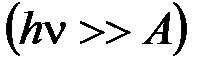 
,
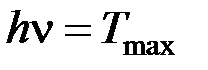, если фотоэффект вызван фотоном, имеющим энергию 
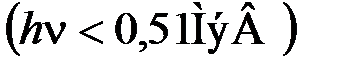, то
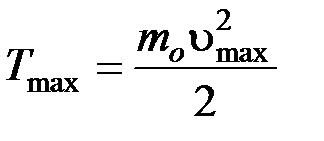, где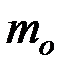 
- масса покоя электрона.
Если фотоэффект вызван фотоном, имеющим энергию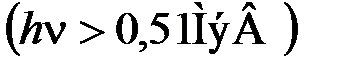 
, то
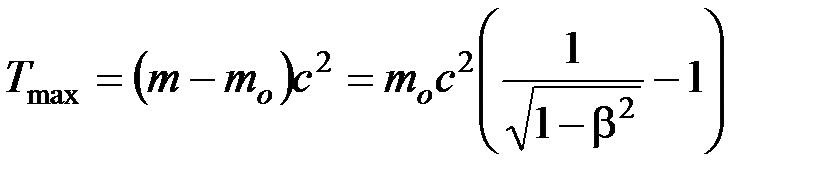, где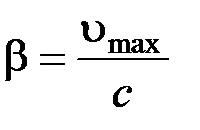 
, 
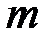- масса релятивистского электрона; 
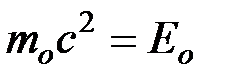- энергия покоя электрона; 
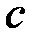- скорость света в вакууме.
|
|
|
Красная граница фотоэффекта
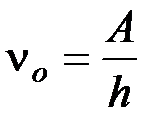или 
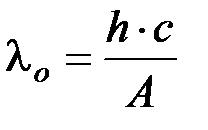, где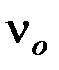 
- минимальная частота света, при которой еще возможен фотоэффект; 
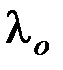- максимальная длина волны света, при которой еще возможен фотоэффект.
Давление, производимое светом при нормальном падении,
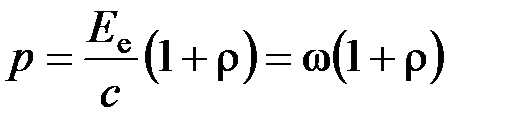, где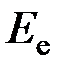 
- облучённость поверхности; 
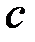- скорость света в вакууме; 
- объемная плотность энергии излучения;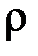 
- коэффициент отражения.
Изменение длины волны при эффекте Комптона
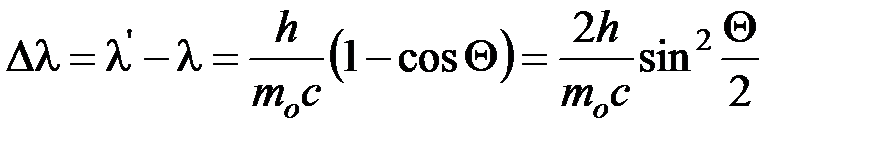, где 
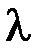- длина волны фотона, испытавшего соударение со свободным или слабосвязанным электроном; 
- длина волны фотона, рассеянного на угол 
после столкновения с электроном;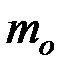 
- масса покоящегося электрона.
Комптоновская длина волны
.
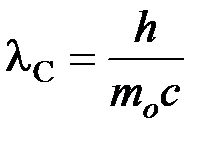Энергия светового фотона равна разности энергий тех стационарных состояний, между которыми совершается квантовый переход электрона:
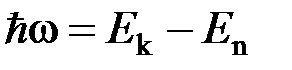, или 
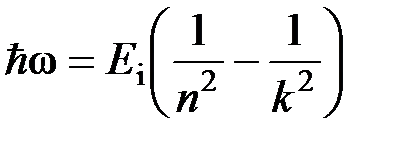, где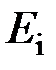 
– энергия ионизации атома водорода (
); 
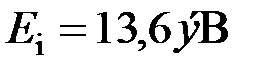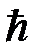- постоянная Планка; 
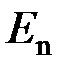– энергия электрона на орбите n; 
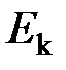– энергия электрона на орбите k; 
– циклическая частота излучения.
Если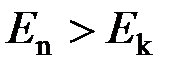 
, фотон излучается, при 
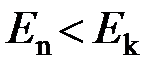наблюдается поглощение фотона с частотой 
.
Модуль момента импульса электрона, движущегося вокруг ядра, кратен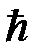 
:
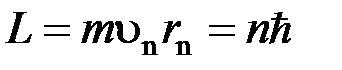, где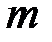 
– масса электрона; 
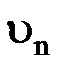- его скорость на n -й орбите; 
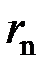- радиус этой орбиты; n =1, 2, 3, …- целое положительное число (главное квантовое число).
Длина волны де Бройля
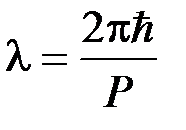, где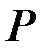 
– модуль импульса частицы.
Модуль импульса частицы и его связь с кинетической энергией T:
а)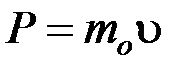 
, 
;
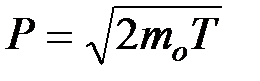б)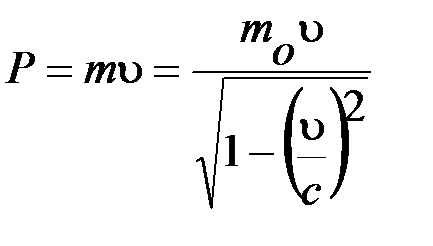 
и 
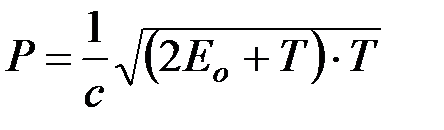, где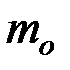 
– масса покоя частицы; 
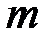– релятивистская масса; 
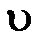- скорость частицы; 
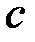– скорость света в вакууме; 
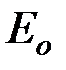– энергия покоя частицы (
).
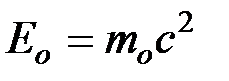Одномерное уравнение Шредингера для стационарных состояний.
|
|
|
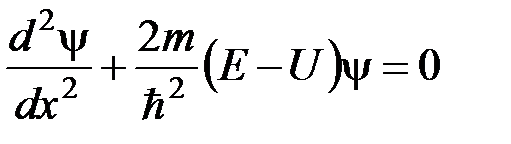, где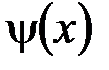 
- волновая функция, описывающая состояние частицы; 
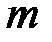– масса частицы; 
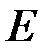– полная энергия; 
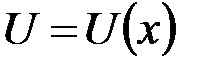- потенциальная энергия частицы.
Вероятность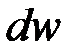 
обнаружить частицу в интервале от x до x + dx (в одномерном случае) выражается формулой
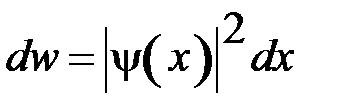, где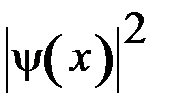 
- плотность вероятности.
Вероятность обнаружить частицу в интервале от x 1 до x 2 находится интегрированием 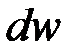в указанных пределах:
.
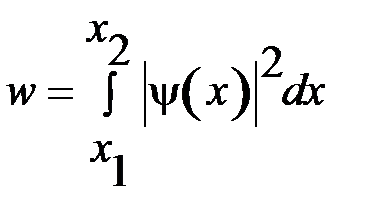Собственное значение энергии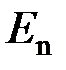 
частицы, находящейся на n -м энергетическом уровне в бесконечно глубоком одномерном прямоугольном потенциальном ящике, определяется формулой
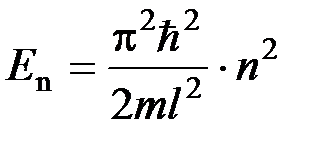(n =1, 2, 3,…), где 
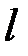- ширина потенциального ящика.
Соответствующая этой энергии собственная волновая функция имеет вид
.
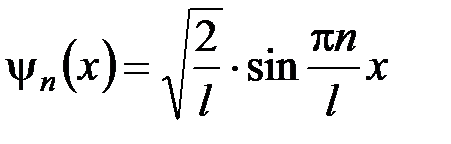Массовое число ядра (число нуклонов в ядре)
,
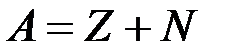где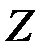 
— зарядовое число (число протонов); 
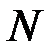— число нейтронов.
