2015-07-14
454
Часть 3. «Оптика. Атомная и ядерная физика.»
Задачи для самостоятельной работы курсантов на практических занятиях
Основные теоретические сведения
Частота колебаний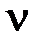 
, длина волны 
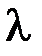и скорость распространения 
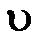света в среде связаны соотношением 
.
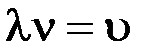Скорость света в сре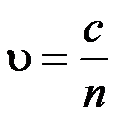де
, где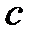 
– скорость света в вакууме; 
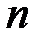– абсолютный показатель преломления среды.
Оптическая длина пути световой волны
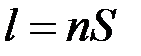, где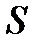 
– геометрическая длина пути в среде с показателем преломления 
.
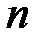Оптическая разность хода двух световых волн
.
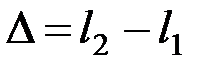Условие максимумов интенсивности света при интерференции
, (
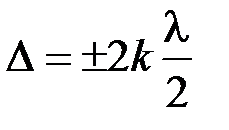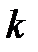=0, 1, 2, 3…).
Условие минимумов интенсивности света при интерференции
, (
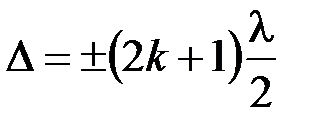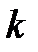=0, 1, 2, 3…).
Связь разности фаз колебаний с оптической разностью хода световых волн
.
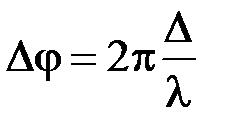Разность хода двух волн, приходящих на экран в опыте Юнга
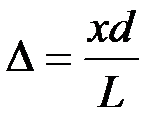, где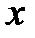 
– координата точки экрана; 
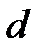– расстояние между источниками, 
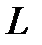– расстояние до экрана.
Координаты максимумов интенсивности (светлых полос) в опыте Юнга
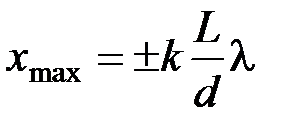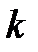, ( =0, 1, 2, 3…).
Координаты минимумов интенсивности
|
|
|
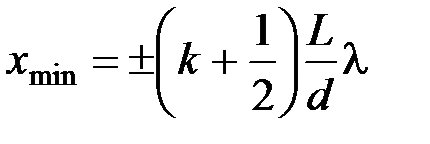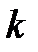, ( =0, 1, 2, 3…).
Расстояние между полосами в опыте Юнга
.
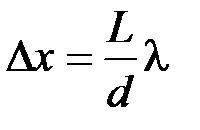Оптическая разность хода световых волн, отраженных от верхней и нижней поверхностей тонкой пластинки или пленки, находящейся в воздухе
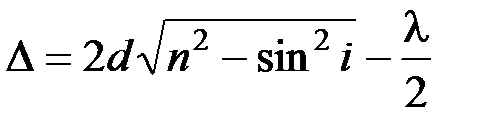или 
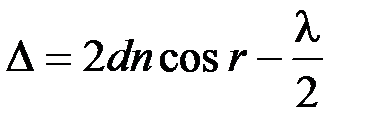, где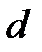 
– толщина пленки; 
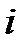– угол падения; 
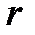– угол преломления.
Второе слагаемое в этих формулах учитывает изменение оптической длины пути световой волны на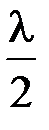 
при отражении ее от среды с большим показателем преломления (оптически более плотной среды).
В проходящем свете отражение световой волны происходит от среды оптически менее плотной и дополнительной разности хода не возникает.
Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем)
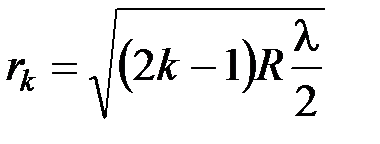, где 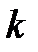– номер кольца ( 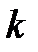=1, 2, 3…); 
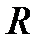– радиус кривизны линзы.
Радиусы темных колец в отраженном свете (или светлых в проходящем)
.
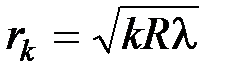Радиус 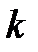-й зоны Френеля для сферической волны
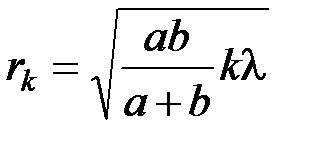, где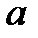 
– расстояние от точечного источника света до фронта волны; 
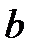– расстояние от фронта волны до точки наблюдения.
Радиус 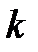-й зоны Френеля для плоской волны
.
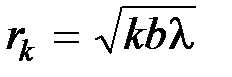Условие максимумов интенсивности при дифракции света на одной щели
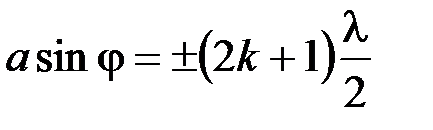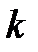, ( =1, 2, 3…), где 
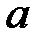– ширина щели; 
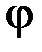– угол дифракции.
Условие минимумов интенсивности при дифракции света на одной щели
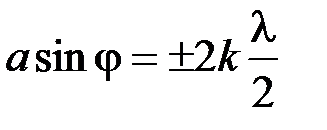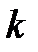, ( =1, 2, 3…).
Условие главных максимумов интенсивности при дифракции света на дифракционной решетке
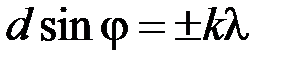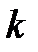( =1, 2, 3…), где 
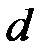– период (постоянная) решетки; 
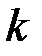– порядок (номер) максимума; 
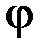– угол дифракции.
