Выделим в дереве какую-нибудь одну вершину, которую назовем корнем. Полученное дерево с выделенной вершиной называется корневым.
Для задания (с точностью до изоморфизма) корневых деревьев используют код из 0 и 1, который мы определим индуктивно.
 Определение. Кодом корневого дерева с одним ребром является
Определение. Кодом корневого дерева с одним ребром является 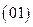 . Пусть деревья
. Пусть деревья 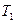 и
и 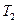 с корнями a и b соответственно (см. рис.) имеют коды
с корнями a и b соответственно (см. рис.) имеют коды 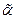 и
и 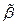 . Тогда кодом дерева
. Тогда кодом дерева 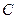 с корнем с является код
с корнем с является код 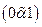 , а кодом дерева
, а кодом дерева 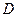 с корнем
с корнем 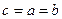 - код
- код 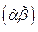 .
.
Пример 1. Написать код дерева, изображенного на рисунке.
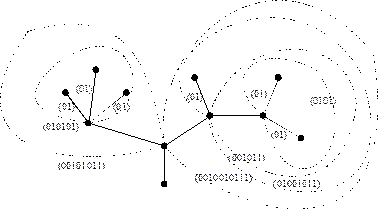 Итак, код дерева -
Итак, код дерева - 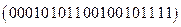 .
.
Справедливо следующее утверждение: для того, чтобы последовательность нулей и единиц являлась кодом некоторого дерева необходимо и достаточно, чтобы число нулей и единиц в этой последовательности было одинаковым, причем в любом начальном отрезке последовательности количество нулей было не меньше количества единиц.
Чтобы построить корневое дерево по коду из нулей и единиц, нужно разбить последовательность на пары 0 и 1, следуя правилу: первая попавшаяся в коде единица образует пару с предшествующим нулем; каждая следующая единица образует пару с ближайшим слева неиспользованным нулем. Если образованные таким образом пары пометить снизу кода фигурными скобками, то каждая такая скобка будет соответствовать ребру графа.
|
|
|
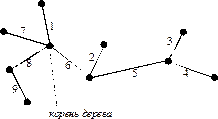 Пример 2. Построить дерево по коду
Пример 2. Построить дерево по коду 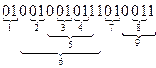 .
.
Для задания помеченных деревьев, т.е. деревьев, вершины которых занумерованы, используют код из натуральных чисел.
Пусть дано помеченное дерево. Чтобы построить его код из натуральных чисел действуем следующим образом. Находим висячую вершину с наименьшим номером. Записываем номер смежной с ней вершины (это начало кода), после чего удаляем эту висячую вершину вместе с инцидентным ей ребром. Для полученного в результате данной операции дерева находим висячую вершину с наименьшим номером, записываем номер смежной с ней вершины (это продолжение кода), после чего удаляем эту висячую вершину вместе с инцидентным ей ребром. Так поступаем до тех пор, пока не останется последнее ребро.
Заметим, что длина кода из натуральных чисел на единицу меньше числа ребер и на две единицы меньше числа вершин данного дерева.
 Пример 3. На рисунке изображено помеченное дерево. Его код
Пример 3. На рисунке изображено помеченное дерево. Его код 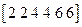 .
.
Построение дерева по коду из натуральных чисел рассмотрим на примере кода 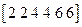 . Прежде всего, заметим, что дерево, которое нам предстоит построить, имеет 8 вершин.
. Прежде всего, заметим, что дерево, которое нам предстоит построить, имеет 8 вершин.
Будем преобразовывать последовательность 224466, действуя по следующей схеме. Вместо первого числа запишем наименьшее натуральное число, которое в этой последовательности не встречается, т.е. 1; получим последовательность 124466. Вместо второго числа в новой последовательности запишем наименьшее, не встречающееся в ней, т.е. 3; получим последовательность 134466, и т.д. Действуем так до тех пор, пока все числа в исходной последовательности не будут заменены. Расположим все последовательности друг под другом; под последней из них запишем код дерева. Выпишем пары вершин, записанные друг под другом в последних двух строчках: (12), (32), (24), (54), (46), (76). Каждая такая пара - это пара концов одного из ребер дерева. Этот список дополняем парой вершин, отсутствующих в предпоследней строчке, т.е. парой (6,8). Теперь строим дерево: отмечаем на плоскости точки – вершины дерева и соединяем их ребрами согласно списку (см. рисунок к примеру 3).
|
|
|
3.11. Остовы графа. Построение минимального остова
Напомним, что подграф 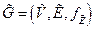 графа
графа 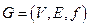 , называется остовным подграфом, если
, называется остовным подграфом, если 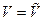 .
.
Определение. Остовом обыкновенного графа называется его остовный подграф, являющийся деревом.
Пусть 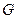 - обыкновенный граф. Упорядочим множество его вершин
- обыкновенный граф. Упорядочим множество его вершин 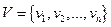 . Определим матрицу Кирхгофа
. Определим матрицу Кирхгофа 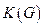 графа
графа 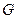 , полагая:
, полагая:
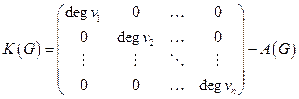 ,
,
где 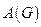 - матрица смежности графа, отвечающая данному упорядочению вершин.
- матрица смежности графа, отвечающая данному упорядочению вершин.
Можно показать, что матрицы Кирхгофа обладают следующим свойством: алгебраические дополнения всех элементов любой из матриц Кирхгофа графа равны между собой.
Утверждение. Число остовов в связном неодноэлементном обыкновенном графе равно алгебраическому дополнению любого элемента его матрицы Кирхгофа.
Доказательство этого утверждения опустим.
Определение. Взвешенным графом будем называть совокупность объектов 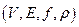 ,где тройка
,где тройка 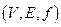 - граф и
- граф и 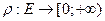 - отображение, называемое весовым.
- отображение, называемое весовым.
Число 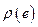 называется весом ребра
называется весом ребра 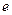 , число
, число 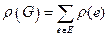 - весом графа
- весом графа 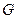 .
.
Определение. Остов 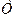 связноговзвешенного графа
связноговзвешенного графа 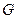 назовем минимальным остовом, если для любого остова
назовем минимальным остовом, если для любого остова 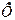 выполнено неравенство
выполнено неравенство 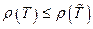 .
.
Рассмотрим задачу о нахождении минимального остова в связном взвешенном графе.
Теорема (алгоритм Краскала). Пусть 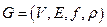 - связный взвешенный граф.
- связный взвешенный граф. 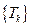 - последовательность его остовных подграфов, заданная индуктивно следующим образом:
- последовательность его остовных подграфов, заданная индуктивно следующим образом:
1. 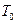 остовный подграф, множество
остовный подграф, множество 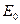 ребер которого пусто.
ребер которого пусто.
2. Пусть 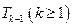 - остовный подграф с множеством ребер
- остовный подграф с множеством ребер 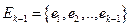 . Тогда
. Тогда 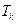 - остовный подграф с множеством ребер
- остовный подграф с множеством ребер 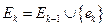 , где ребро
, где ребро 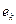 выбирается из множества
выбирается из множества 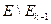 так, что выполнены два условия: а) добавление ребра
так, что выполнены два условия: а) добавление ребра 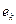 не приводит к образованию циклов; б) из ребер, удовлетворяющих условию а), ребро
не приводит к образованию циклов; б) из ребер, удовлетворяющих условию а), ребро 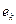 обладает наименьшим весом.
обладает наименьшим весом.
Тогда последним элементом последовательности 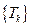 является минимальный остов графа
является минимальный остов графа 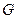 .
.
Доказательство теоремы опустим.
Замечания. 1. Если граф несвязен, то по алгоритму Краскала строится остовный лес.
2. Если граф невзвешен, то, присваивая всем ребрам одинаковые веса, мы можем применить алгоритм Краскала для построения остова (остовного леса).
Пример 1. Построить остов минимального веса графа 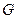 с множеством вершин
с множеством вершин 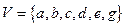 ; множеством ребер
; множеством ребер 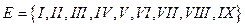 ; отображением инцидентности
; отображением инцидентности 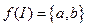 ,
, 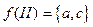 ,
, 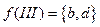 ,
, 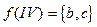 ,
, 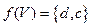 ,
, 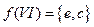 ,
, 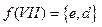 ,
, 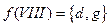 ,
, 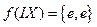 и весовым отображением
и весовым отображением 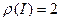 ,
, 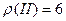 ,
, 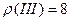 ,
, 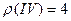 ,
, 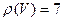 ,
, 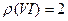 ,
, 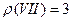 ,
, 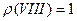 .
.
Согласно алгоритму Краскала строим последовательность остовных подграфов:
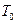 с пустым множеством ребер;
с пустым множеством ребер;
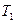 с множеством ребер
с множеством ребер 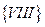 ;
;
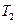 с множеством ребер
с множеством ребер 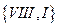 ;
;

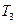 с множеством ребер
с множеством ребер 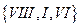 ;
;
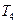 с множеством ребер
с множеством ребер 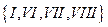 ;
;
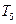 с множеством ребер
с множеством ребер 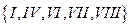 .
.
Добавление к графу 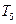 любого из оставшихся ребер графа
любого из оставшихся ребер графа 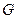 ведет к образованию цикла. Таким образом, подграф
ведет к образованию цикла. Таким образом, подграф 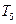 c множеством ребер
c множеством ребер 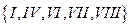 , - минимальный остов, вес которого равен
, - минимальный остов, вес которого равен 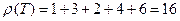 .
.
 2015-07-14
2015-07-14 7908
7908







