Пусть 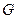 - произвольный неориентированный граф, а
- произвольный неориентированный граф, а 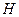 - его подграф. С каждой вершиной
- его подграф. С каждой вершиной 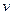 и каждым ребром
и каждым ребром 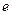 графа
графа 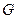 можно связать подграфы
можно связать подграфы 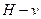 ,
, 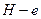 и
и 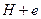 .
.
1. Подграф 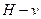 получается из подграфа
получается из подграфа 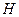 удалением вершины
удалением вершины 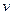 и всех инцидентных этой вершине ребер. Отметим, что если
и всех инцидентных этой вершине ребер. Отметим, что если 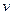 не входит в множество вершин графа
не входит в множество вершин графа 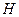 , то
, то 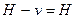 .
.
2. Подграф 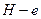 получается из подграфа
получается из подграфа 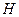 удалением ребра
удалением ребра 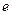 и всех инцидентных этой вершине ребер. Если
и всех инцидентных этой вершине ребер. Если 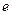 не входит в множество ребер графа
не входит в множество ребер графа 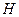 , то
, то 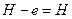 .
.
3. Подграф 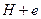 получается из подграфа
получается из подграфа 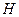 добавлением ребра
добавлением ребра 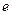 и двух его концевых вершин. Если
и двух его концевых вершин. Если 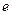 входит в множество ребер графа
входит в множество ребер графа 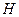 , то
, то 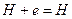 .
.
4. Говорят, что граф 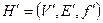 получен из графа
получен из графа 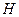 путем подразбиения ребра
путем подразбиения ребра 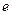 , если
, если
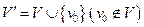 ,
,
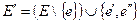
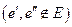 ,
, 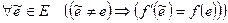 ,
,
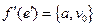 ,
, 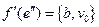 , где
, где 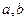 - концы ребра
- концы ребра 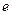 .
.
 |
Пример 2.
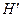 - граф, полученный из графа
- граф, полученный из графа 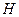 путем подразбиения ребра
путем подразбиения ребра 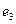 .
.
Пусть 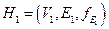 и
и 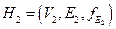 - подграфы графа
- подграфы графа 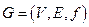 .
.
6. Пересечением графов 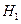 и
и 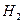 называется граф
называется граф 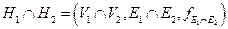 .
.
7. Объединением графов 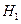 и
и 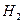 называется граф
называется граф 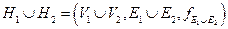 .
.
Аналогично определяется пересечение и объединение любого конечного числа подграфов.
Определение. Пусть 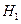 ,
, 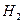 ,…,
,…, 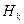 - непустые подграфы графа
- непустые подграфы графа 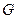 и выполнены условия:
и выполнены условия:
1. 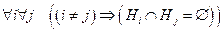 ;
;
2. 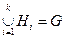 .
.
Тогда семейство множеств 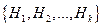 называется дизъюнктным разбиением графа
называется дизъюнктным разбиением графа 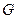 .
.
3.4. Маршруты, цепи и циклы в графе
Определение. Маршрутом длины 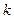 на графе
на графе 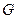 называется такая последовательность
называется такая последовательность 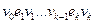 вершин и ребер графа, в которой
вершин и ребер графа, в которой 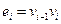
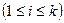 .
.
Такой маршрут кратко называют 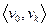 -маршрутом и кратко обозначают
-маршрутом и кратко обозначают 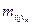 . Про
. Про 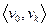 -маршрут говорят, что он соединяет вершину
-маршрут говорят, что он соединяет вершину 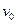 с вершиной
с вершиной 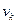 . Вершины
. Вершины 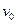 и
и 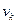 называют соответственно началом и концом маршрута.
называют соответственно началом и концом маршрута.
Случай, когда длина маршрута равна нулю, не исключается; в этом случае маршрут сводится к одной вершине.
Если 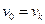 , то маршрут называется замкнутым.
, то маршрут называется замкнутым.
Заметим, что в обыкновенном графе маршрут полностью определяется последовательностью 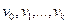 своих вершин.
своих вершин.
В произвольном маршруте любое ребро и любая вершина могут повторяться. Накладывая ограничения на число повторений вершин и ребер, приходим к следующим частным видам маршрутов.
Определение. Цепь – это маршрут без повторяющихся ребер.
Цепь, соединяющую вершину 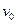 с вершиной
с вершиной 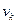 , кратко называют
, кратко называют 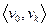 -цепью и обозначают
-цепью и обозначают 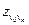 .
.
Определение. Цепь называется простой, если в ней нет повторяющихся вершин за исключением, быть может, совпадающих концевых.
Определение. Замкнутая цепь называется циклом.
Определение. Замкнутая простая цепь называется простым циклом.
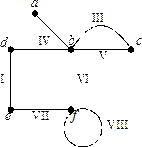 Пример 1.
Пример 1. 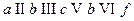 -
- 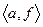 -маршрут; его длина равна 4; данный маршрут является
-маршрут; его длина равна 4; данный маршрут является 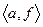 -цепью; эта цепь незамкнутая, не простая. Маршрут
-цепью; эта цепь незамкнутая, не простая. Маршрут 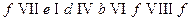 - цикл длины 5, этот цикл не является простым;
- цикл длины 5, этот цикл не является простым; 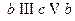 - простой цикл.
- простой цикл.
Лемма (о простой цепи). Если для некоторых вершин 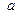 и
и 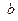 на графе
на графе 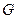 существует
существует 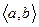 -маршрут, то существует и простая
-маршрут, то существует и простая 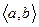 - цепь.
- цепь.
Доказательство. Рассмотрим в графе 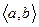 -маршрут наименьшей длины. Покажем, что этот маршрут является простой цепью. Будем рассуждать от противного. Пусть в нашем маршруте имеется повторяющаяся вершина
-маршрут наименьшей длины. Покажем, что этот маршрут является простой цепью. Будем рассуждать от противного. Пусть в нашем маршруте имеется повторяющаяся вершина 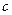 . Тогда, заменяя часть маршрута от первого вхождения вершины
. Тогда, заменяя часть маршрута от первого вхождения вершины 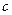 до ее второго вхождения на одну вершину
до ее второго вхождения на одну вершину 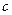 , мы получим более короткий
, мы получим более короткий 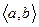 -маршрут. Получили противоречие ■
-маршрут. Получили противоречие ■
Лемма (об инвертировании маршрута). Если для некоторых вершин 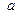 и
и 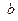 на графе
на графе 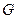 существует
существует 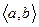 -маршрут, то существует и
-маршрут, то существует и 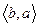 - маршрут.
- маршрут.
Данное утверждение настолько очевидно, что вряд ли нуждается в доказательстве.
 2015-07-14
2015-07-14 1308
1308








