ПП 11. Производная Функции
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ
Производной функции 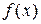 в точке
в точке 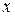 называется
называется 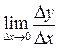 при условии, что он существует. Обозначение:
при условии, что он существует. Обозначение: 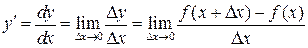 .
.
Геометрический смысл производной.
Уравнение касательной к кривой 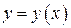 в точке
в точке 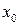 :
:
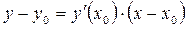 .
.
Тангенс угла наклона касательной к оси ОХ:
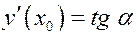
Уравнение нормали имеет вид:
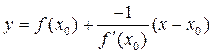 .
.
Правила и формулы дифференцирования
1) 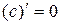 ,
, 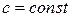 ;
;
2) 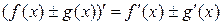 ;
;
3) 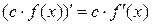 ;
;
4) 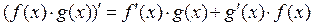 ;
;
5) 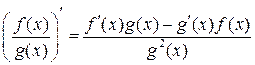 ,
, 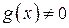 .
.
Производная обратной функции:
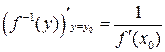
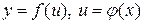 , тогда
, тогда 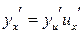
Таблица производных
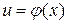 | ||
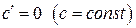 | ||
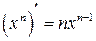 | 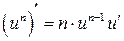 . . | |
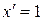 | ||
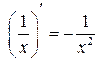 | ||
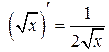 | ||
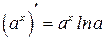 | 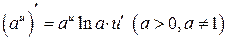 | |
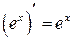 | 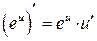 | |
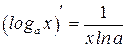 | 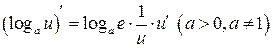 | |
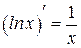 | 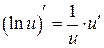 | |
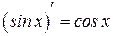 | 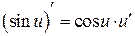 | |
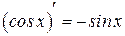 | 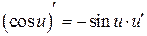 | |
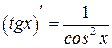 | 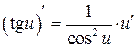 | |
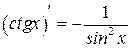 | 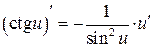 | |
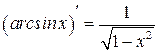 | 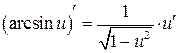 | |
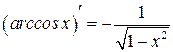 | 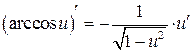 | |
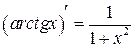 | 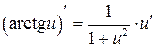 | |
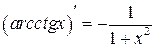 | 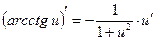 | |
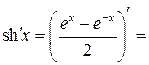 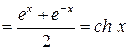 | 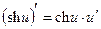 | |
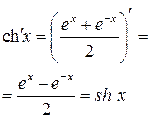 | 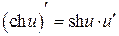 | |
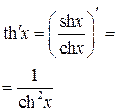 | 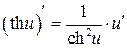 | |
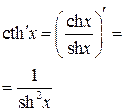 | 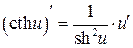 |
Производные высших порядков
Производная второго порядка: 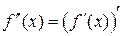
Производная 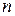 -го порядка:
-го порядка: 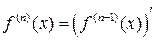 или
или 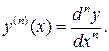
Логарифмическая производная:
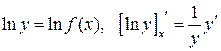 ,
, 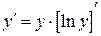 .
.
Производная неявной функции:
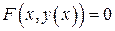 ,
, 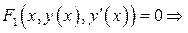
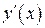 .
.
Для отыскания второй производной соотношение 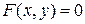 дифференцируем два раза по переменной
дифференцируем два раза по переменной 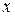 , считая
, считая 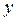 функцией
функцией 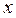 , и выражаем
, и выражаем 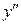 как функцию
как функцию 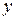 и
и 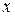 .
.
Производные функции, заданной параметрически:
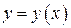
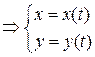
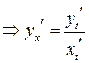 - первая,
- первая,
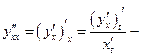 вторая.
вторая.
Правила вычисления производной n -го порядка
1. 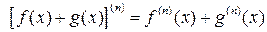 .
.
2. Формула Лейбница (производная произведения):
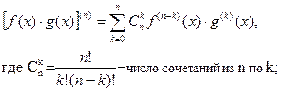
где 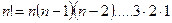 ,
,  .
.
| пп 11. Теоретические Упражнения | ||||
| ТУ ПП 11. №1. | Пользуясь только определением производной, найдите производную функции 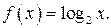 РЕШЕНИЕ: РЕШЕНИЕ: 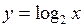 , , 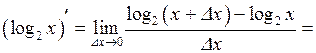 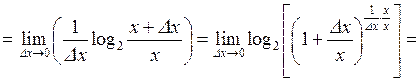 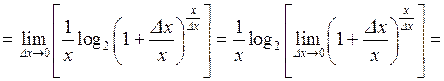 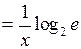 , , 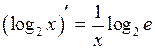 . . | 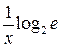 | ||
| ТУ ПП 11. №2. | Для заданной 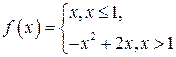 , , 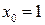 найдите найдите 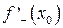 и и 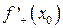 . Решение: Имеем . Решение: Имеем 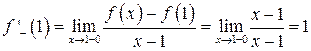 и и 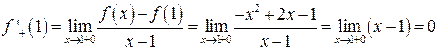 . . | 1,0 | ||
| ТУ ПП 11. №3. | Пусть 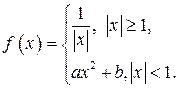 . Найдите коэффициенты . Найдите коэффициенты 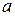 и и 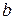 такие, чтобы функция такие, чтобы функция 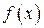 была непрерывна и дифференцируема в любой точке. Решение: Рассмотрим поведение была непрерывна и дифференцируема в любой точке. Решение: Рассмотрим поведение 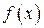 в окрестности точки в окрестности точки 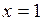 . Пусть . Пусть 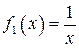 , , 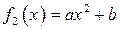 . Тогда для непрерывности . Тогда для непрерывности 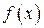 необходимо необходимо 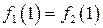 , , 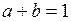 . Для дифференцируемости необходимо . Для дифференцируемости необходимо 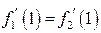 , , 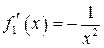 , , 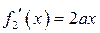 , , 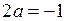 . Решая полученную систему для коэффициентов квадратичной функции, получаем . Решая полученную систему для коэффициентов квадратичной функции, получаем 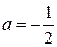 , , 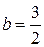 . . | 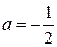 , , 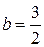 . . | ||
| ТУ ПП 11. №4. | Докажите, что производная четной функции – функция нечетная, а производная нечетной – функция четная. Решение: 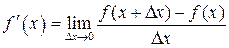 . Пусть . Пусть 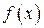 четна, четна, 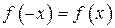 . Тогда . Тогда 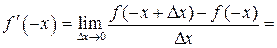 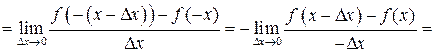 (обозначим (обозначим 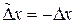 , , 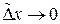 при при 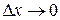 ) ) 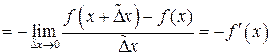 , , 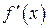 нечетна. Если нечетна. Если 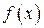 нечетна, нечетна, 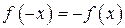 , то , то 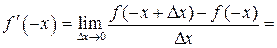 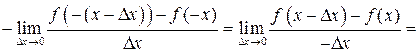 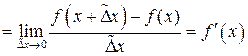 , , 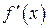 четна. четна. | |||
| ТУ ПП 11. №5. | Пусть 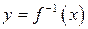 – функция, обратная заданной – функция, обратная заданной 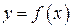 . Выразите . Выразите 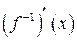 через через 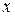 и и 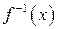 , если , если 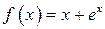 . Решение: Если . Решение: Если 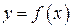 , то , то 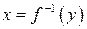 ; ; 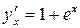 , , 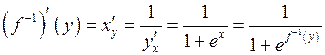 . Обозначая аргумент обратной функции через . Обозначая аргумент обратной функции через 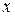 , получаем , получаем 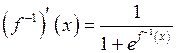 . . | 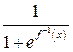 | ||
| ТУ ПП 11. №6. | Покажите, что функция 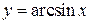 удовлетворяет дифференциальному уравнению удовлетворяет дифференциальному уравнению 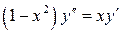 . Решение: . Решение: 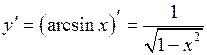 , , 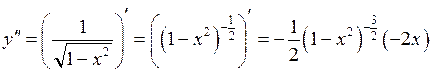 . . 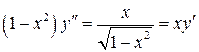 . . | |||
| пп 11. Производная Функции | ||||
| ПП 11. №1. | Найдите 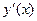 , если , если 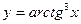 . Решение: . Решение: 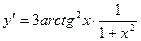 . . | |||
| ПП 11. №2. | Найдите 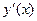 , если , если 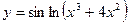 . Решение: . Решение: 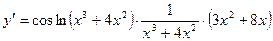 | |||
| ПП 11. №3. | Найдите 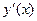 , если , если 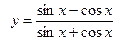 . Решение: . Решение: 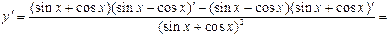 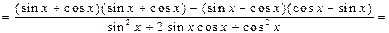 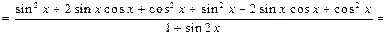 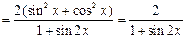 . . | |||
| ПП 11. №4. | Найдите 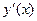 , если , если  . Решение: . Решение: 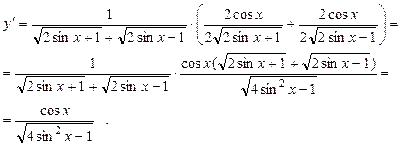 | |||
| ПП 11. №5. | Найдите 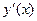 , если , если 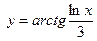 . Решение: . Решение: 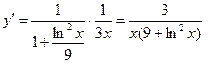 . . | |||
| ПП 11. №6. | Найдите 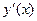 , если , если 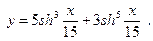 Решение: Решение: 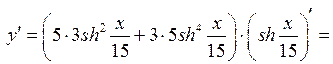 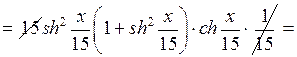 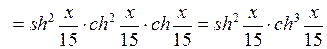 . . | |||
| ПП 11. №7. | Найдите 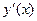 , если , если 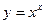 . Решение: . Решение: 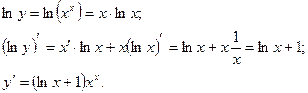 | |||
| ПП 11. №8. | Найдите 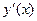 , если , если 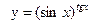 . Решение: Применяем метод логарифмического дифференцирования. . Решение: Применяем метод логарифмического дифференцирования. 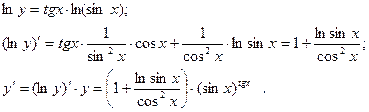 | |||
| ПП 11. №9. | Найдите 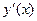 , если , если 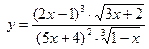 . Решение: . Решение: 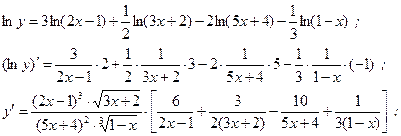 | |||
| ПП 11. №10. | Найдите 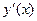 , если , если 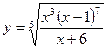 . Решение: . Решение: 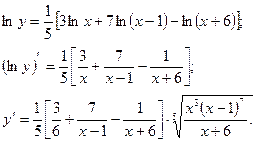 | |||
| ПП 11. №11. | Вычислите производную 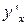 функции функции 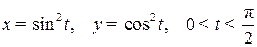 , заданной параметрически. Решение: Воспользуемся формулой для производной функции, заданной параметрически: , заданной параметрически. Решение: Воспользуемся формулой для производной функции, заданной параметрически: 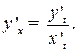 Вычислим производные по переменной Вычислим производные по переменной 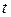 : : 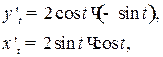 отсюда отсюда 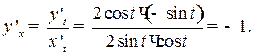 | -1 | ||
| ПП 11. №12. | Найдите 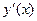 , если , если 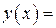 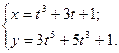 Решение: Решение: 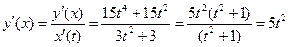 | 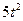 | ||
| ПП 11. №13. | Составьте уравнения касательной и нормали к кривой 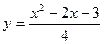 в точке в точке 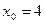 . Решение: . Решение: 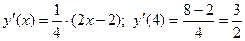 ; ; 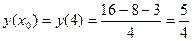 . Уравнение касательной: . Уравнение касательной: 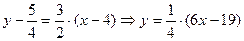 . Уравнение нормали: . Уравнение нормали: 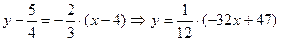 . . | |||
| ПП 11. №14. | Составьте уравнение касательной к графику функции: 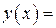 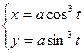 в точке в точке 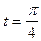 . Решение: . Решение: 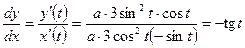 . При . При 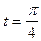 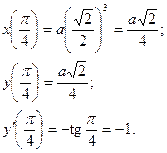 Уравнение касательной Уравнение касательной 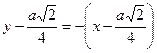 или или 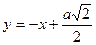 . . | |||
| ПП 11. №15. | Найдите производную 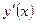 функции функции 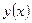 , если она задана неявно уравнением , если она задана неявно уравнением 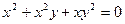 . Решение: Дифференцируем равенство по . Решение: Дифференцируем равенство по 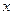 : : 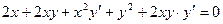 . Отсюда . Отсюда 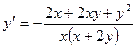 . . | 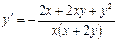 | ||
| ПП 11. №16. | 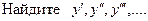 , если , если 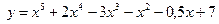 . Решение: . Решение: 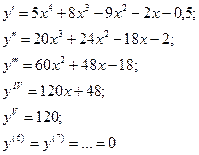 | |||
| ПП 11. №17. | Найдите производную n – го порядка от функции 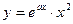 . Решение: . Решение: 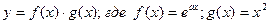 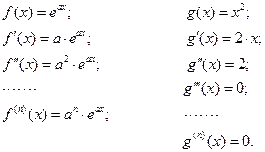 Таким образом, в формуле Лейбница всего 3 ненулевых члена. Вычисляем коэффициенты: Таким образом, в формуле Лейбница всего 3 ненулевых члена. Вычисляем коэффициенты: 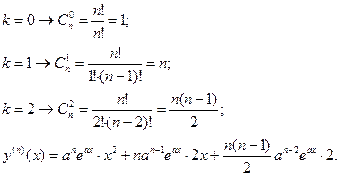 | 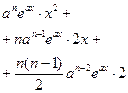 | ||
| ПП 11. №18. | 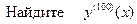 , если , если 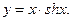 Решение: Воспользуемся формулой Лейбница. Решение: Воспользуемся формулой Лейбница. 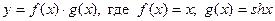 . . 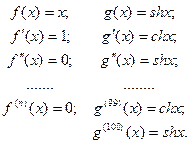 В формуле Лейбница ненулевыми будут только два слагаемых: при В формуле Лейбница ненулевыми будут только два слагаемых: при 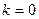 ; ; 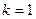 . . 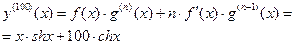 | 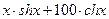 | ||
| ПП 11. №19. | Найдите 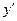 и и 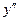 функции, заданной параметрически: функции, заданной параметрически: 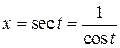 , , 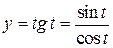 , , 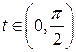 . Решение: . Решение: 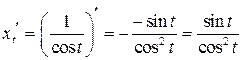 , , 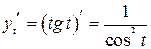 . . 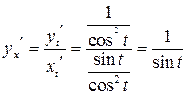 . . 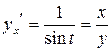 . . 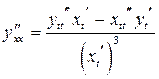 ; ; 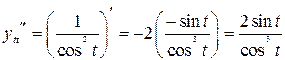 , , 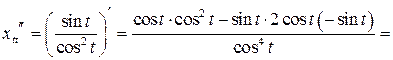 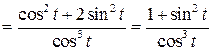 . . 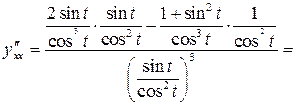 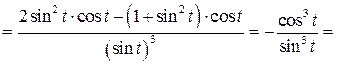 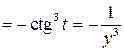 . . |  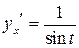 или или 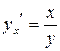 . . 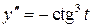 или или 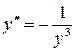 , , 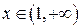 | ||
| ПП 11. №20. | Найдите 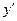 и и 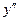 функции, заданной неявно: функции, заданной неявно: 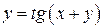 . Решение: дифференцируем уравнение по . Решение: дифференцируем уравнение по 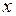 : : 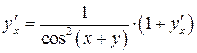 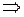 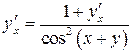 , , 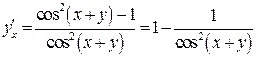 , , 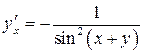 , Используя , Используя 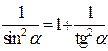 , получаем , получаем 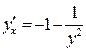 . Повторно дифференцируя по . Повторно дифференцируя по 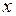 , получаем , получаем 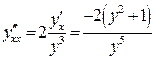 . . | 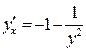 , , 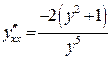 . . | ||
 2015-07-14
2015-07-14 4192
4192