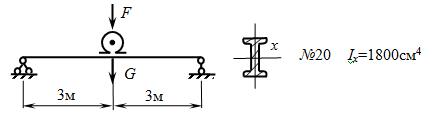
Решение:
Балка находится под действием двух нагрузок: под действием статической нагрузки – веса двигателя G и под действием динамической (вибрационной) нагрузки F. Поэтому все параметры складываются из статической и динамической составляющих:
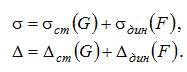
Статические составляющие от силы G найдем как обычно при статическом расчете:
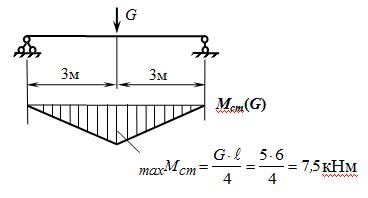
Наибольшее статическое напряжение в среднем сечении балки будет:
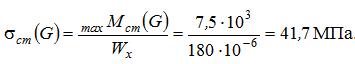
Для определения статического прогиба среднего сечения выберем вспомогательное состояние и построим эпюру  :
:
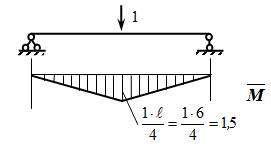
Прогиб от статической нагрузки G будет:
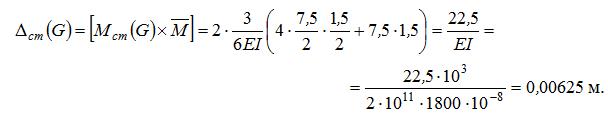
Динамические значения параметров от действия вибрационной нагрузкиопределяются с помощью динамического коэффициента следующим образом:
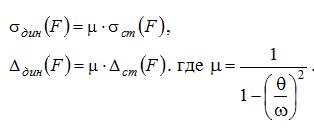
В формулу динамического коэффициента вибрационной нагрузки входит величина ω – круговая частота собственных (свободных) колебаний, определяемая по формуле:
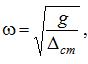
где: g=9,81м/сек2 – ускорение свободного падения,
Δ ст – перемещение точки расположения колеблющейся массы (в данном случае двигателя) от собственного веса.
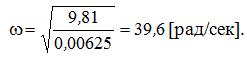
Тогда значение динамического коэффициента вибрационной нагрузки будет:
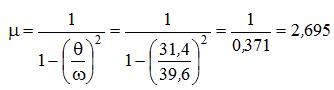
Здесь круговая частота действия самой вибрационной нагрузки
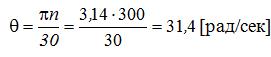
Далее находим 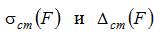 , для чего к балке прикладывается наибольшая величина вибрационной нагрузки статическим образом:
, для чего к балке прикладывается наибольшая величина вибрационной нагрузки статическим образом:
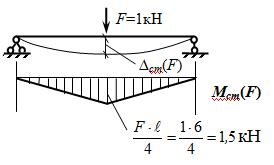
Прогиб середины пролета в балке на двух опорах можно вычислить и по известной формуле:
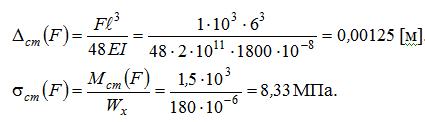
Тогда динамические значения искомых параметров будут:
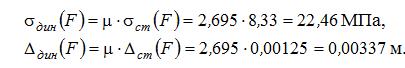
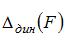 представляет собой амплитуду колебаний массы (двигателя), то есть наибольшее отклонение от положения статического равновесия. Поэтому наибольшее значение прогиба складывается из статического смещения
представляет собой амплитуду колебаний массы (двигателя), то есть наибольшее отклонение от положения статического равновесия. Поэтому наибольшее значение прогиба складывается из статического смещения 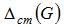 и амплитуды колебаний
и амплитуды колебаний 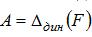
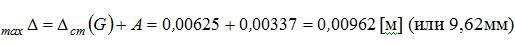
 2015-07-14
2015-07-14 1564
1564







