Производная и ее механический(физический смысл). Теорема о непрерывности функции, имеющей производную.
Касательная и нормаль к кривой. Геометрический смысл производной. Уравнения касательной и нормали к графику функции.
Правила дифференцирования: суммы, произведения и частного двух функций; сложной функции; обратной функции. Производные основных элементарных функций(таблица производных).
Понятие функции, заданной параметрически. Производная параметрически заданной функции. Дифференциал функции и его связь с производной. Дифференциал суммы, произведения и частного двух функций. Дифференциал сложной функции(инвариантность формы дифференциала). Приближенное вычисление приращения функции с помощью дифференциала.
Производная второго порядка и ее механический(физический) смысл.
Образец варианта на уровень А
1. 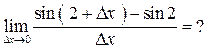
2. 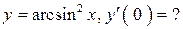
3. 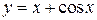 . Вычислить
. Вычислить 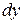 в точке
в точке 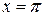 при
при 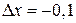 .
.
4. 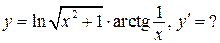
5. 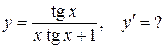
6. 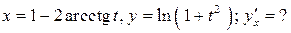
7. Составить уравнение нормали к кривой 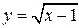 в точке с ординатой
в точке с ординатой 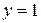 .
.
Тренировочные варианты на уровни В, С
Вариант 1
1. 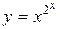 .
. 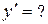 (Ответ:
(Ответ: 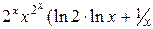 )
)
2. 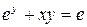 .
. 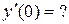 (Ответ:
(Ответ: 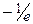 )
)
3. В какой точке кривой 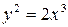 касательная перпендикулярна прямой
касательная перпендикулярна прямой 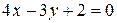 ? (Ответ: (
? (Ответ: (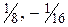 ))
))
Вариант 2
1. 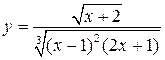 .
. 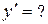 (Ответ:
(Ответ: 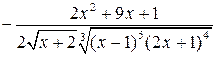 )
)
2. 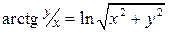 .
. 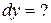 (Ответ:
(Ответ: 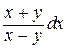 )
)
3. Найти углы, под которыми пересекаются кривые 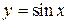 и
и 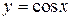 ,
, 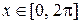 . (Ответ:
. (Ответ: 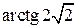 )
)
Вариант 3
1. 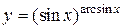 .
. 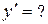 (Ответ:
(Ответ: 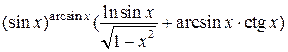 )
)
2. 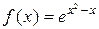 . Найти приближенно (с помощью дифференциала)
. Найти приближенно (с помощью дифференциала) 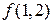 .
.
(Ответ: 1,2)
3. Составить уравнение такой нормали к параболе 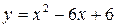 , которая перпендикулярна к прямой, соединяющей начало координат с вершиной параболы. (Ответ:
, которая перпендикулярна к прямой, соединяющей начало координат с вершиной параболы. (Ответ: 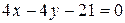 )
)
 2015-07-14
2015-07-14 471
471






