2015-07-14
1547
Магнитное поле в веществе может создаваться двумя способами:
1. макроскопическими токами проводимости (ток по проводникам)
2. микротоками обусловленными движением электронов в атомах и молекулах.
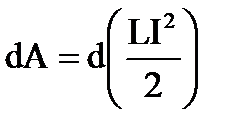Все вещества обладают магнитными свойствами. Вещество или тело рассматриваются с точки зрения магнитных свойств – магнетик.
Намагничивание – явление возникновения объектного макроскопического магнитного момента. Намагничивание характеризуется намагниченностью. Намагниченность (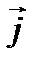
) – есть магнитный момент единицы объема.
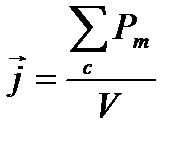
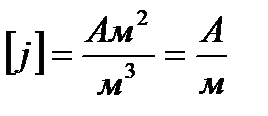Pм=IS
В вакууме молекулярные токи отсутствуют и jвакуум=0
Вектор магнитной индукции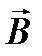 
создает макротоки и микротоки.
Существует три вида микроскопических магнитных моментов.
1. Электронный орбитальный магнитный момент – из-за вращения электронов вокруг ядер.
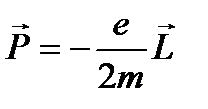
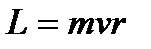
2. Электронный спиновой магнитный момент.
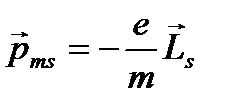, где Ls – спиновой механический момент.
3. Ядерный магнитный момент.
Электронный орбитальный магнитный момент зависит от состояния электронов, и он либо равен 0 или порядка момента Бора:
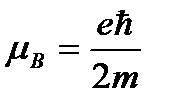
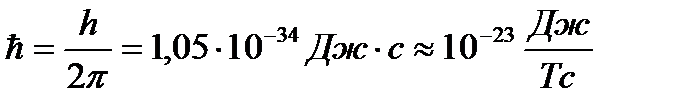
Спиновый магнитный момент = моменту Бора.
Ядерный магнитный момент на 2 или3 порядка меньше магнетона Бора.
В атомах и молекулах магнитные моменты отдельных электронов либо полностью, либо частично скомпенсированы, поэтому могнитный момент атомов, молекул =0 или????? 2-3 магнитона Бора.
3 7. Напряженность магнитного поля.
Теорема о циркуляции вектора магнитной индукции в вакууме (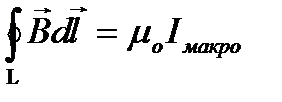
) допускает обобщение на магнитное поле в веществе в виде
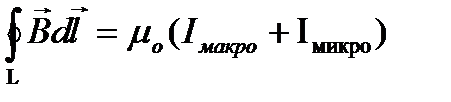,где Iмакро и Iмикро – алгебраическая сумма макро и микро токов через поверхность S ограниченных контуром L.
Покажем теперь, что Iмикро связан с намагниченностью j: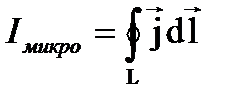 
Т.е. сумма микро токов через поверхность S ограниченных контуром L равна циркуляции вектора намагниченности j.
Рассмотрим прямой круговой намагниченный цилиндр длинной dl и площадью поперечного сечения S.
Молекулярные токи внутри цилиндра текут в противоположные стороны и поэтому взаимноскомпенсированы. Нескомпенсированы только те токи, которые выходят на поверхность цилиндра и ни складываются в поверхностный ток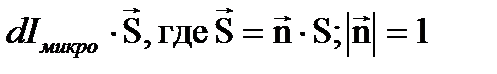 
С другой стороны полный магнитный момент цилиндра по определению намагниченности равен: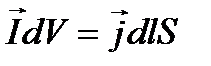 
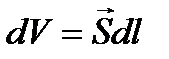
Так как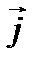 
и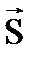 
направлены в одну сторону, то dIмикро=jdl.
Вклад в циркуляцию намагниченность дадут только те токи, которые нанизаны как бусы на нитку. Тогда окончательно можно написать: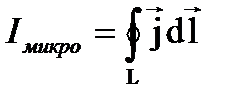
С учетом последнего соотношения теорема о циркуляции вектора магнитной индукции принимает вид: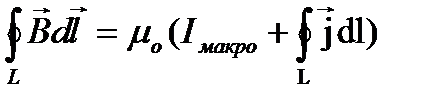 
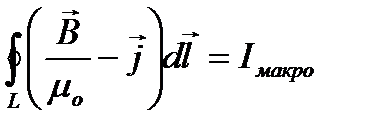
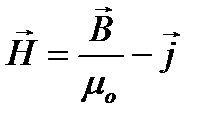
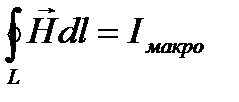- теорема о циркуляции магнитного поля
Циркуляция вектора напряженности магнитного поля вдоль произвольного замкнутого конура равна результирующему макро току через поверхность ограниченного этим контуром. Для изотропных магнетиков связь намагниченности j и напряженности Н магнитного поля. Т.е.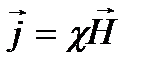 
χ—безразмерная величина – магнитная восприимчивость среды или вещества. Подставим 
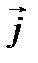в выражении для 
:
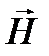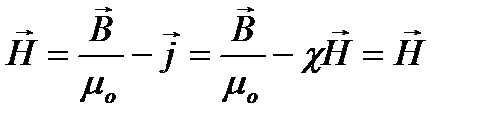
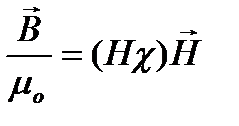
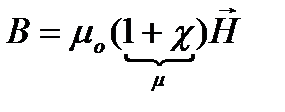
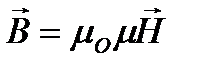
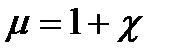
Если среда не изотропная, то μ становиться тензором: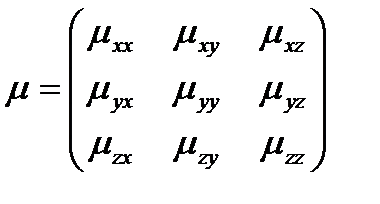 
В электричестве векторы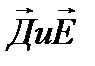 
описывают поле:
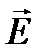- является истинным, он порождается и связанный поляризованными зарядами.
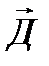- вспомогательный вектор
В магнетизме:
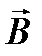- истинный – порождается микро и макро токами
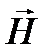- только макроскопическими токами
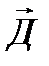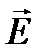Природа вектора и 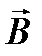и и 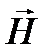одинаковы.
