Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.
13
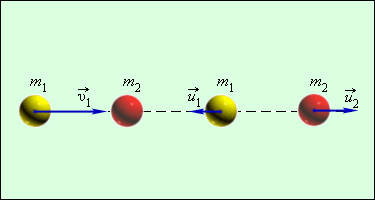
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.
 По закону сохранения механической энергии По закону сохранения механической энергии 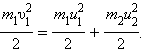 |
Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде:
| m 1υ1 = m 1 u 1 + m 2 u 2. |
Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u 1 и u 2 шаров после столкновения:
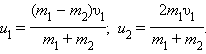 |
В частном случае, когда оба шара имеют одинаковые массы (m 1 = m 2), первый шар после соударения останавливается (u 1 = 0), а второй движется со скоростью u 2 = υ1, т. е. шары обмениваются скоростями (и, следовательно, импульсами).
14
Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению) на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр. Более точно момент силы частицы определяется как векторное произведение:
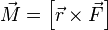 где
где 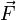 — сила, действующая на частицу, а
— сила, действующая на частицу, а 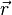 — радиус-вектор частицы.
— радиус-вектор частицы.
Если имеется материальная точка 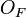 , к которой приложена сила
, к которой приложена сила  , то момент силы относительно точки
, то момент силы относительно точки 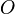 равен векторному произведению радиус-вектора
равен векторному произведению радиус-вектора 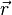 , соединяющего точки
, соединяющего точки 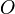 и
и 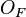 , на вектор силы
, на вектор силы 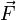 :
:
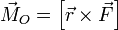 .
.
Момент силы относительно оси равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси относительно точки пересечения оси с плоскостью, т.е. Mz(F) = Mo(F') = F' h'.
15
Моме́нт и́мпульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массывращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение[1].
Момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.
Псевдовектор — величина, компоненты которой преобразуются как вектор при поворотах системы координат, но меняющие свой знак противоположно тому, как ведут себя компоненты вектора при любой инверсии (обращении знака) координат. Т.е. псевдовектор меняет направление на противоположное при сохранении абсолютной величины (домножается на минус единицу) при любой инверсии координатной системы.
Псевдоскаляр — величина, не изменяющаяся при переносе и повороте координатных осей, но изменяющая свой знак при замене направления одной оси на противоположное (и вообще - при переходе к базису другой ориентации).
Момент импульса замкнутой системы сохраняется. Момент импульса является одним из трёх аддитивных (энергия, импульс, момент импульса) интегралов движения.
Момент импульса 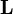 материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
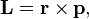
где 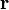 — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,
— радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, 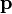 — импульс частицы.
— импульс частицы.
16
Моме́нт ине́рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
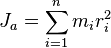 ,
,
где: mi — масса i -й точки, ri — расстояние от i -й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
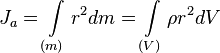 ,
,
где: dm = ρ dV — масса малого элемента объёма тела dV, ρ — плотность, r — расстояние от элемента dV до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
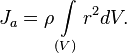
Теорема Гюйгенса — Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
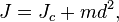 где m — полная масса тела.
где m — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
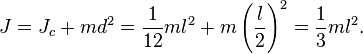
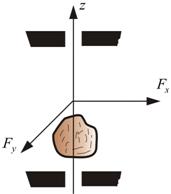
Составляющие 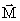 – момента внешних сил, направленные вдоль x и y, компенсируются моментами сил реакции закрепления. Вращение вокруг оси z происходит только под действием Mz.
– момента внешних сил, направленные вдоль x и y, компенсируются моментами сил реакции закрепления. Вращение вокруг оси z происходит только под действием Mz.
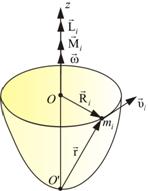
Пусть некоторое тело вращается вокруг оси z (рис. 6.5).
 |  |
| Рис. 6.4 | Рис. 6.5 |
Получим уравнение динамики для некоторой точки mi этого тела, находящегося на расстоянии Ri от оси вращения. При этом помним, что 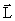 и
и 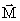 направлены всегда вдоль оси вращения z, поэтому
направлены всегда вдоль оси вращения z, поэтому
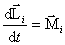 или
или 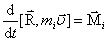 .
.
Поскольку 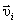 у всех точек разная, введем вектор угловой скорости
у всех точек разная, введем вектор угловой скорости 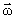 , причем
, причем 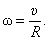 . Тогда
. Тогда
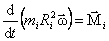 .
.
Так как тело абсолютно твердое, то в процессе вращения mi и Ri останутся неизменными. Тогда
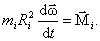
Обозначим Ii – момент инерции точки находящейся на расстоянии R от оси вращения:
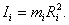 . . |
Момент инерции тела служит мерой инертности во вращательном движении.
В общем случае тело состоит из огромного количества точек, и все они находятся на разных расстояниях от оси вращения. Момент инерции такого тела равен:
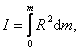 . . | (6.2.2) |
Как видно, момент инерции I – величина скалярная.
Просуммировав (6.2.1) по всем i -м точкам, получим 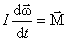 или
или
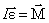 . . |
Это основное уравнение динамики тела, вращающегося вокруг неподвижной оси. (Сравним: 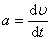 – основное уравнение динамики поступательного движения тела).
– основное уравнение динамики поступательного движения тела).
Для момента импульса 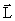 тела, вращающегося вокруг оси z, имеем:
тела, вращающегося вокруг оси z, имеем:
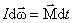 , , 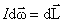 , , 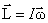 . . | (6.2.4) |
(Сравним: 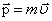 –для поступательного движения).
–для поступательного движения).
При этом помним, что 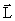 и
и 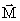 - динамические характеристики вращательного движения, направленные всегда вдоль оси вращения. Причем
- динамические характеристики вращательного движения, направленные всегда вдоль оси вращения. Причем 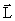 определяется направлением вращения, как и
определяется направлением вращения, как и 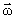 , а направление
, а направление 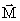 зависит от того, ускоряется или замедляется вращение.
зависит от того, ускоряется или замедляется вращение.
18
Кинетическая энергия – величина аддитивная. Поэтому кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек, на которые это тело можно мысленно разбить:
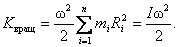 , , |
Если тело вращается вокруг неподвижной оси z с угловой скоростью 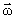 , то линейная скорость i -й точки
, то линейная скорость i -й точки 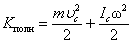 , Ri – расстояние до оси вращения. Следовательно,
, Ri – расстояние до оси вращения. Следовательно, 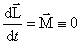
Сопоставив формулы выше, можно увидеть, что момент инерции тела I является мерой инертности при вращательном движении, так же как масса m – мера инерции при поступательном движении.
В общем случае движение твердого тела можно представить в виде суммы двух движений – поступательного со скоростью vc и вращательного с угловой скоростью ω вокруг мгновенной оси, проходящей через центр инерции. Тогда полная кинетическая энергия этого тела
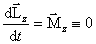 , , | (6.4.3) |
Здесь Ic – момент инерции относительно мгновенной оси вращения, проходящей через центр инерции.
Для замкнутой системы тел момент внешних сил всегда равен нулю, так как внешние силы вообще не действуют на замкнутую систему.
Поэтому 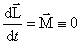 , то есть
, то есть 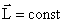 или
или 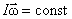
Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.
Это один из фундаментальных законов природы.
Аналогично для замкнутой системы тел, вращающихся вокруг оси z:
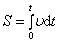 отсюда
отсюда 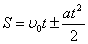 или
или 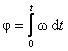 .
.
Если момент внешних сил относительно неподвижной оси вращения тождественно равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения.
Момент импульса и для незамкнутых систем постоянен, если результирующий момент внешних сил, приложенных к системе, равен нулю.
Очень нагляден закон сохранения момента импульса в опытах с уравновешенным гироскопом – быстро вращающимся телом, имеющим три степени свободы.
Используется гироскоп в различных навигационных устройствах кораблей, самолетов, ракет (гирокомпас, гирогоризонт). Один из примеров навигационного гироскопа изображен на рисунке.
Именно закон сохранения момента импульса используется танцорами на льду для изменения скорости вращения. Или еще известный пример – скамья Жуковского.
Изученные нами законы сохранения есть следствие симметрии пространства-времени.
Принцип симметрии был всегда путеводной звездой физиков, и она их не подводила.
Но вот в 1956 г. Ву Цзянь, обнаружил асимметрию в слабых взаимодействиях: он исследовал β-распад ядер изотопа СO 60 в магнитном поле и обнаружил, что число электронов, испускаемых вдоль направления магнитного поля, не равно числу электронов, испускаемых в противоположном направлении.
В этом же году Л. Ледерман и Р. Гарвин (США) обнаружили нарушение симметрии при распаде пионов и мюонов.
Эти факты означают, что законы слабого взаимодействия не обладают зеркальной симметрией.
20
Колебаниями называются движения или процессы, характеризующиеся определенной повторяемостью во времени. Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Исследование гармонических колебаний важно по двум причинам:
1) колебания, которые встречаются в природе и технике, часто имеют близкий к гармоническому характер;
2) различные периодические процессы (процессы, которые повторяются через равные промежутки времени) можно представить как суперпозицию (наложение) гармонических колебаний. Гармонические колебания некоторой величины s описываются уравнением вида
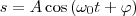 (1) где ω0 — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ — начальная фаза колебания в момент времени t=0, (ω0t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А.
(1) где ω0 — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ — начальная фаза колебания в момент времени t=0, (ω0t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А.
Определенные состояния системы, которая совершает гармонические колебания, повторяются через промежуток времени Т, имеющий название период колебания, за который фаза колебания получает приращение (изменение) 2π, т. е.
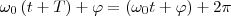
откуда 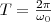 (2)
(2)
Величина, обратная периоду колебаний, 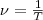 (3)
(3)
т. е. число полных колебаний, которые совершаются в единицу времени, называется частотой колебаний. Сопоставляя найдем
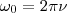
Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, во время которого за 1 с совершается один цикл процесса.
Найдем первую и вторую производные по времени от величины s, совершающей гармонические колебания:
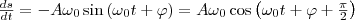 (4)
(4)
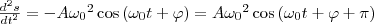 (5)
(5)
т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин в формулах (4) и (5) соответственно равны Аω0 и Аω02. Фаза величины в формуле (4) отличается от фазы величины в формуле (1) на π/2, а фаза величины в выражении (5) отличается от фазы величины (1) на π. Значит, в моменты времени, когда s=0, ds/dt имеет наибольшие значения; когда же s становится равным максимальному отрицательному значению, то d2s/dt2 равен наибольшему положительному значению.
21
Пружинный маятник — это груз массой m, который подвешен на абсолютно упругой пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника имеет вид
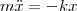 или
или 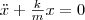
Из формулы (1) вытекает, что пружинный маятник совершает гармонические колебания по закону х = Асоs(ω0t+φ) с циклической частотой
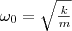 (2) и периодом
(2) и периодом 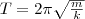 (3)
(3)
Формула (3) верна для упругих колебаний в границах, в которых выполняется закон Гука, т. е. если масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, используя (2) и формулу потенциальной энергии предыдущего раздела, равна
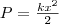
2. Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела.
Если маятник из положения равновесия отклонили на некоторый угол α, то, используя уравнение динамики вращательного движения твердого тела, момент M возвращающей силы
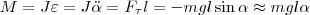 (4) где J — момент инерции маятника относительно оси, которая проходит через точку подвеса О, l – расстояние между осью и центром масс маятника, Fτ ≈ –mgsinα ≈ –mgα — возвращающая сила (знак минус указывает на то, что направления Fτ и α всегда противоположны; sinα ≈ α поскольку колебания маятника считаются малыми, т.е. маятника из положения равновесия отклоняется на малые углы). Уравнение (4) запишем как
(4) где J — момент инерции маятника относительно оси, которая проходит через точку подвеса О, l – расстояние между осью и центром масс маятника, Fτ ≈ –mgsinα ≈ –mgα — возвращающая сила (знак минус указывает на то, что направления Fτ и α всегда противоположны; sinα ≈ α поскольку колебания маятника считаются малыми, т.е. маятника из положения равновесия отклоняется на малые углы). Уравнение (4) запишем как
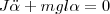 или
или 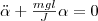 .Принимая
.Принимая 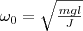 (5) получим уравнение
(5) получим уравнение 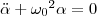 идентичное с (1), решение которого (1) найдем и запишем как:
идентичное с (1), решение которого (1) найдем и запишем как:  (6).
(6).
Из формулы (6) вытекает, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω0 и периодом
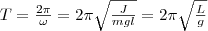 (7) где введена величина L=J/(m l) — приведенная длина физического маятника.
(7) где введена величина L=J/(m l) — приведенная длина физического маятника.
Точка О' на продолжении прямой ОС, которая отстоит от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качаний физического маятника (рис. 1). Применяя теорему Штейнера для момента инерции оси, найдем 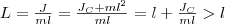 т. е. ОО' всегда больше ОС. Точка подвеса О маятника и центр качаний О' имеют свойство взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О подвеса будет новым центром качаний, и при этом не изменится период колебаний физического маятника.
т. е. ОО' всегда больше ОС. Точка подвеса О маятника и центр качаний О' имеют свойство взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О подвеса будет новым центром качаний, и при этом не изменится период колебаний физического маятника.
3. Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити. Момент инерции математического маятника
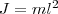 (8) где l — длина маятника.
(8) где l — длина маятника.
Поскольку математический маятник есть частный случай физического маятника, если предположить, что вся его масса сосредоточена в одной точке — центре масс, то, подставив (8) в (7), найдем выражение для периода малых колебаний математического маятника
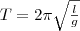 (9) Сопоставляя формулы (7) и (9), видим, что если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Значит, приведенная длина физического маятника — это длина такого математического маятника, у которого период колебаний совпадает с периодом колебаний данного физического маятника.
(9) Сопоставляя формулы (7) и (9), видим, что если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Значит, приведенная длина физического маятника — это длина такого математического маятника, у которого период колебаний совпадает с периодом колебаний данного физического маятника.
22
Колеблющееся тело может принимать участие в нескольких колебательных процессах, тогда следует найти результирующее колебание, другими словами, колебания необходимо сложить. В данном разделе будем складывать гармонические колебания одного направления и одинаковой частоты
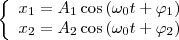 применяя метод вращающегося вектора амплитуды, построим графически векторные диаграммы этих колебаний (рис. 1). Taк как векторы A1 и A2 вращаются с одинаковой угловой скоростью ω0, то разность фаз (φ2 - φ1) между ними будет оставаться постоянной. Значит, уравнение результирующего колебания будет
применяя метод вращающегося вектора амплитуды, построим графически векторные диаграммы этих колебаний (рис. 1). Taк как векторы A1 и A2 вращаются с одинаковой угловой скоростью ω0, то разность фаз (φ2 - φ1) между ними будет оставаться постоянной. Значит, уравнение результирующего колебания будет 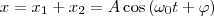 (1)
(1)
В формуле (1) амплитуда А и начальная фаза φ соответственно определяются выражениями
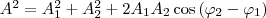 (2)
(2) 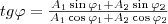 . Значит, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает при этом также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ2 - φ1) складываемых колебаний.
. Значит, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает при этом также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ2 - φ1) складываемых колебаний.
Исследуем выражение (2) в зависимости от разности фаз (φ2 - φ1):
1) φ2 - φ1 = ±2mπ (m = 0, 1, 2,...), тогда A=A1+A2, т. е. амплитуда результирующего колебания А будет равна сумме амплитуд складываемых колебаний;
2) φ2 - φ1 = ±(2m+1)π (m = 0, 1, 2,...), тогда A=|A1–A2|, т. е. амплитуда результирующего колебания будет равна разности амплитуд складываемых колебаний.
Периодические изменения амплитуды колебания, которые возникают при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω<<ω. Выберем начало отсчета так, чтобы начальные фазы обоих колебаний были равны нулю:
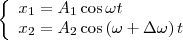 Складывая эти выражения и учитывая, что во втором сомножителе Δω/2<<ω, получим
Складывая эти выражения и учитывая, что во втором сомножителе Δω/2<<ω, получим
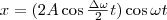 (3) Результирующее колебание (3) можно считать как гармоническое с частотой ω, амплитуда Аσ которого изменяется по следующему периодическому закону:
(3) Результирующее колебание (3) можно считать как гармоническое с частотой ω, амплитуда Аσ которого изменяется по следующему периодическому закону:
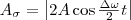 (4) Частота изменения Аσ в два раза больше частоты изменения косинуса (так как берется по модулю), т. е. частота биений равна разности частот складываемых колебаний:
(4) Частота изменения Аσ в два раза больше частоты изменения косинуса (так как берется по модулю), т. е. частота биений равна разности частот складываемых колебаний:
 . Период биений
. Период биений 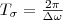 .
.
При исследовании сложного колебательного процесса нужно знать, что любые сложные периодические колебания s=f(t) можно представить в виде суперпозиции (наложения) одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, которые кратны циклической частоте ω0:
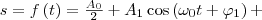
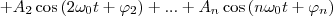 (5)
(5)
Представление в виде (5) любой периодической функции связывают с понятием гармонического анализа сложного периодического колебания, или разложения Фурье. Слагаемые ряда Фурье, которые определяют гармонические колебания с частотами ω0, 2ω0, 3ω0,..., называются первой (или основной), второй, третьей и т. д. гармониками сложного периодического колебания.
23
Найдем результат сложения двух гармонических колебаний одинаковой частоты ω, которые происходят во взаимно перпендикулярных направлениях вдоль осей х и у. Начало отсчета для простоты выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем это в виде
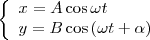 (1)
(1)
где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t. Записывая складываемые колебания как
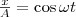
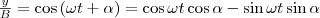 и заменяя во втором уравнении
и заменяя во втором уравнении  на
на 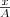 и
и 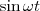 на
на 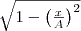 , найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей:
, найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей:
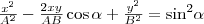 (2)
(2)
Поскольку траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.
Размеры осей эллипса и его ориентация зависят от амплитуд складываемых колебаний и разности фаз α. Рассмотрим некоторые частные случаи, которые представляют для нас физический интерес:
1) α = mπ (m=0, ±1, ±2,...). В этом случае эллипс становится отрезком прямой
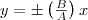 (3)
(3)
где знак плюс соответствует нулю и четным значениям m (рис. 1а), а знак минус — нечетным значениям m (рис. 2б). Результирующее колебание есть гармоническое колебание с частотой ω и амплитудой, которое совершается вдоль прямой (3), составляющей с осью х угол. В этом случае имеем дело с линейно поляризованными колебаниями;
2) α = (2m+1)(π/2) (m=0, ± 1, ±2,...). В этом случае уравнение станет иметь вид
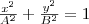 (4)
(4)
Это есть уравнение эллипса, у которого оси совпадают с осями координат, а его полуоси равны соответствующим амплитудам (рис. 2). Если А=В, то эллипс (4) превращается в окружность. Такие колебания называются циркулярно поляризованными колебаниями или колебаниями, поляризованными по кругу.
24
Попробуем получить уравнение волны, чтобы получить смещение точки в любой момент времени при распространении гармонической волны. Сделаем это на примере волны бегущей по шнуру. Ось Ох направим по направлению распространения волны. Конец шнура заставим совершать колебания с частотой ω. Тогда колебания будут происходить по закону:
s = Sm*sin(ω*t).
Колебания будут распространяться вдоль шнура со скоростью V. Произвольной точки шнура эти колебания достигнут через время равное
τ = x/V.
Эта точка тоже начнет совершать гармонические колебания с такой же частотой ω. Но при этом будут запаздывать на время τ.
Если считать, что волна не затухает по мере распространения, то колебания в произвольной точке х будут совершаться с такой же амплитудой Sm, но с другой фазой.
Уравнение бегущей волны будет иметь следующий вид:
S = Sm*sin(ω*(t-τ)) = Sm*sin(ω*(t- x/V)).
25
Если в среде распространяется несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Волны накладываются друг на друга, не возмущая (не искажая друг друга). Это и есть принцип суперпозиции волн.
Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называется стоячей волной. Практически стоячие волны возникают при отражении от преград.
Напишем уравнения двух плоских волн, распространяющихся в противоположных направлениях (начальная фаза ф=0):
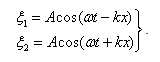 Сложим уравнения и преобразуем по формуле суммы косинусов (5.4.3):
Сложим уравнения и преобразуем по формуле суммы косинусов (5.4.3):
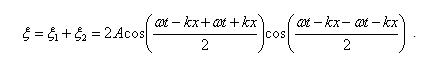 Т.к.
Т.к. 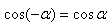 , то можно записать:
, то можно записать: 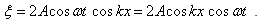
Учитывая, что 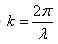 , получим уравнение стоячей волны:
, получим уравнение стоячей волны: 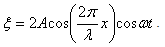
В выражении для фазы не входит координата, поэтому можно записать: 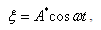 где суммарная амплитуда
где суммарная амплитуда 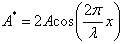 .
.
В точках, где координаты удовлетворяют условию 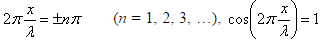 , суммарная амплитуда равна максимальному значению:
, суммарная амплитуда равна максимальному значению: 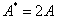 , – это пучности стоячей волны. Координаты пучностей:
, – это пучности стоячей волны. Координаты пучностей: 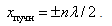
В точках, координаты которых удовлетворяют условию 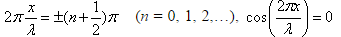 , и суммарная амплитуда колебаний равна нулю
, и суммарная амплитуда колебаний равна нулю 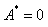 , – это узлы стоячей волны. Координаты узлов:
, – это узлы стоячей волны. Координаты узлов: 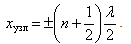
Точки среды, находящиеся в узлах, колебаний не совершают.
Если рассматривать бегущую волну, то в направлении ее распространения переносится энергия колебательного движения. В случае же стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях.
26
Идеальный газ - это физическая модель газа, взаимодействие между молекулами которого пренебрежительно мало.
Свойства идеального газа:
- взаимодействие между молекулами пренебрежительно мало
- расстояние между молекулами много больше размеров молекул
- молекулы - это упругие шары
- отталкивание молекул возможно только при соударении
- движение молекул - по законам Ньютона
- давление газа на стенки сосуда - за счет ударов молекул газа
Основное уравнение МКТ связывает микропараметры частиц (массу молекулы, среднюю кинетическую энергию молекул, средний квадрат скорости молекул) с макропараметрами газа (р - давление, V - объем, Т - температура).
Давление газа на стенки сосуда пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
Ниже приведены различные выражения для основного уравнения МКТ: 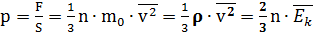
где р - давление газа на стенки сосуда(Па)
n - концентрация молекул, т.е. число молекул в единице объема (1/м3)
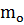 - масса молекулы (кг)
- масса молекулы (кг) 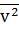 - средний квадрат скорости молекул (м2/с2)
- средний квадрат скорости молекул (м2/с2)
ρ - плотность газа (кг/м3) 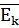 - средняя кинетическая энергия молекул (Дж)
- средняя кинетическая энергия молекул (Дж)
Давление идеального газа на стенки сосуда зависит от концентрации молекул и пропорционально средней кинетической энергии молекул.
 2015-07-14
2015-07-14 818
818







