Вес — сила воздействия тела на опору (или подвес или другой вид крепления), препятствующую падению, возникающая в поле сил тяжести (В случае нескольких опор под весом понимается суммарная сила, действующая на все опоры; впрочем, для жидких и газообразных опор в случае погружения тела в них часто делается исключение, т. е. тогда силы воздействия тела на них исключают из веса и включают в силу Архимеда[1]).
Единица измерения веса в Международной системе единиц (СИ) — ньютон, иногда используется единица СГС —дина.
Вес P тела, покоящегося в инерциальной системе отсчёта 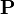 , совпадает с силой тяжести, действующей на тело, и пропорционален массе
, совпадает с силой тяжести, действующей на тело, и пропорционален массе 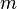 и ускорению свободного падения
и ускорению свободного падения 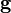 в данной точке:
в данной точке:
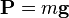
При движении системы тело — опора (или подвес) относительно инерциальной системы отсчёта c ускорением 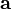 вес перестаёт совпадать с силой тяжести:
вес перестаёт совпадать с силой тяжести:
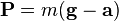
Вес можно измерять с помощью пружинных весов, которые могут служить и для косвенного измерения массы, если их соответствующим образом проградуировать; рычажные весы в такой градуировке не нуждаются, так как в этом случае сравниваются массы, на которые действует одинаковое ускорение свободного падения или сумма ускорений в неинерциальных системах отсчёта. При взвешивании с помощью технических пружинных весов вариациями ускорения свободного падения обычно пренебрегают, так как влияние этих вариаций обычно меньше практически необходимой точности взвешивания.
На вес тела в жидкой или газообразной среде влияет также сила Архимеда, таким образом, вес тела, погружённого в среду, уменьшается на вес вытесненного объёма среды; в случае, если плотность тела меньше плотности среды, вес становится отрицательным (то есть на тело действует выталкивающая сила). Сила Архимеда может оказать влияние и на взвешивание с помощью рычажных весов, если сравниваются тела с различной плотностью.
Состояние отсутствия веса (невесомость) наступает при удалении тела от притягивающего объекта, либо когда тело находится в свободном падении, то есть 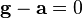 .
.
Си́лаупру́гости — сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное состояние.
В случае упругих деформаций является потенциальной. Сила упругости имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. В простейшем случае растяжения/сжатия тела сила упругости направлена противоположно смещению частиц тела, перпендикулярно поверхности.
Вектор силы противоположен направлению деформации тела (смещению его молекул). Если исчезает деформация тела, то исчезает и сила упругости.
В Международной системе единиц (СИ) сила упругости так же, как и все другие силы, измеряется в ньютонах
В простейшем случае одномерных малых упругих деформаций формула для силы упругости имеет вид:
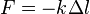 ,
,
где 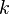 — жёсткость тела,
— жёсткость тела, 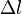 — величина деформации.
— величина деформации.
Жесткость тела зависит от его формы и размеров, а также от материала, из которого оно изготовлено.
В словесной формулировке закон Гука звучит следующим образом:
Сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению тела и направлена противоположно направлению перемещения частиц тела относительно других частиц при деформации.
При увеличении величины деформации закон Гука перестаёт действовать, сила упругости начинает сложным образом зависеть от величины растяжения или сжатия
Для тонкого растяжимого стержня закон Гука имеет вид:
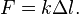
Здесь 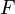 — сила, которой растягивают (сжимают) стержень,
— сила, которой растягивают (сжимают) стержень, 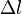 — абсолютное удлинение (сжатие) стержня, а
— абсолютное удлинение (сжатие) стержня, а 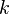 — коэффициент упругости (или жёсткости).
— коэффициент упругости (или жёсткости).
Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения 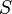 и длины
и длины 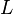 ) явно, записав коэффициент упругости как
) явно, записав коэффициент упругости как
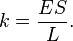
Величина 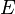 называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.
называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.
Если ввести относительное удлинение
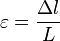
и нормальное напряжение в поперечном сечении
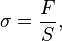
то закон Гука для относительных величин запишется как
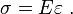
В такой форме он справедлив для любых малых объёмов материала.
Также при расчёте прямых стержней применяют запись закона Гука в относительной форме
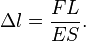
Закон Гука применим в области упругих деформаций (в области небольших деформаций),
то есть до достижения предела текучести твердого тела, иначе до границы, после которой
деформации становятся необратимыми после снятия нагрузки.
Как гласит закон Гука, отношение нагрузки к напряжению для данного образца в пределах
упругой зоны является константой.
 2015-07-14
2015-07-14 12814
12814
