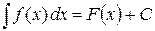 , где
, где 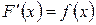 и
и 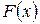 называется первообразной.
называется первообразной.
1. 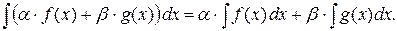
2. 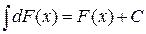 . 4.
. 4. 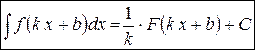
| № | Табличные интегралы | № | Табличные интегралы |
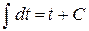 . .
| 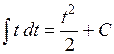
| ||
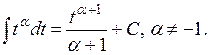
| 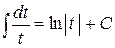 . .
| ||
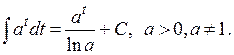
| 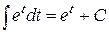 . .
| ||
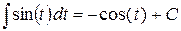
| 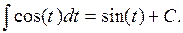
| ||
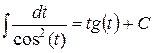 . .
| 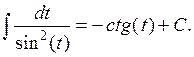
| ||
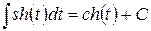 . .
| 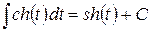
| ||
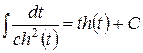 . .
| 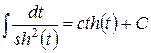 . .
| ||
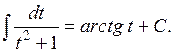
| 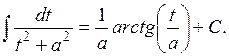
| ||
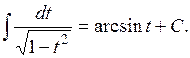
| 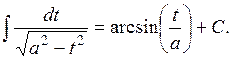
| ||
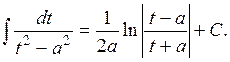
| 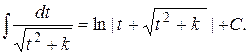
| ||
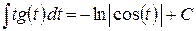 . .
| 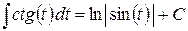 . .
|
Определенный интеграл: 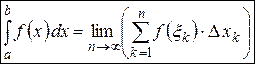 .
.
Формула Ньютона-Лейбница: 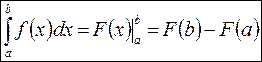 , частн. сл.
, частн. сл. 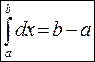 .
.
| Способы вычисления неопределенного интеграла | ||||||||||||
| Замена переменной | 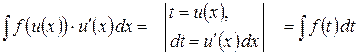 .
Частный случай: .
Частный случай: 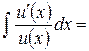 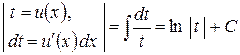 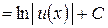 . .
| |||||||||||
| Метод подстановки | 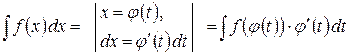 . .
| |||||||||||
| Интегрирование по частям | 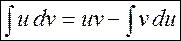
| |||||||||||
1. 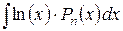 ; ;
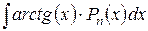 ; ;
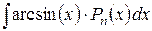 ; ;
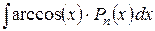 . .
| 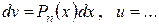 ,
где ,
где 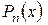 – многочлен степени n. – многочлен степени n.
| |||||||||||
2. 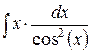 , ,
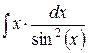 . .
| 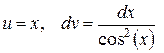 ; ;
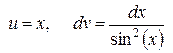 . .
| |||||||||||
3. 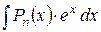 ; ;
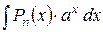 ; ;
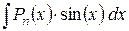 ; ;
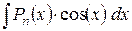 . .
| 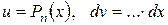 ,
n раз интегрировать по частям. ,
n раз интегрировать по частям.
| |||||||||||
4. 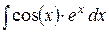 ; ;
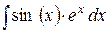 ; ;
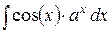 ; ;
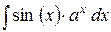 . .
| 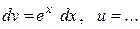 ,
Дважды проинтегрировав по частям,
получим в результате искомый интеграл. Составить уравнение из исходного выражения и полученного, где роль переменной играет искомый интеграл. Выражая искомый интеграл, получить ответ. ,
Дважды проинтегрировав по частям,
получим в результате искомый интеграл. Составить уравнение из исходного выражения и полученного, где роль переменной играет искомый интеграл. Выражая искомый интеграл, получить ответ.
| |||||||||||
| Интегрирование рациональных функций | ||||||||||||
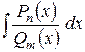 , где , где 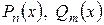 - многочлены соответственно степени - многочлены соответственно степени 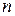 и и 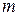 . .
| ||||||||||||
Если 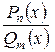 – неправильная дробь ( – неправильная дробь (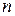 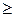 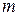 ), то необходимо выделить целую часть: ), то необходимо выделить целую часть: 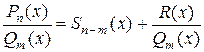 , где , где 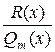 – правильная дробь. – правильная дробь.
| ||||||||||||
Знаменатель разложить на линейные и квадратичные множители, для последних дискриминант 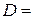 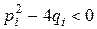 : :
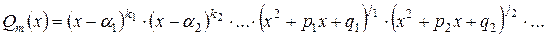 . .
| ||||||||||||
Правильную дробь всегда можно разложить на простейшие дроби типа:
1) 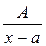 , 2) , 2) 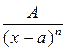 , 3) , 3) 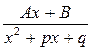 , 4) , 4) 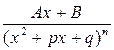 , , 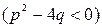 . .
 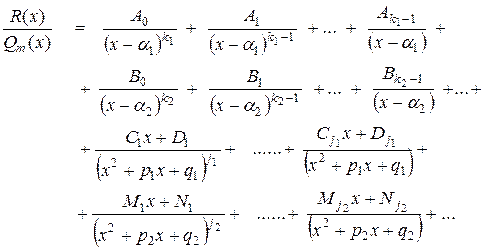 После умножения на
После умножения на 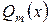 искомые коэффициенты разложения находятся из условия тождественного равенства двух многочленов.
Для линейных множителей: искомые коэффициенты разложения находятся из условия тождественного равенства двух многочленов.
Для линейных множителей: 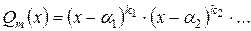 коэффициенты можно вычислить по формулам: коэффициенты можно вычислить по формулам:
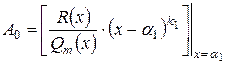 , , 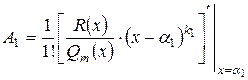 , , 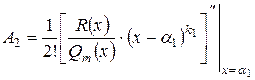 , …, , …, 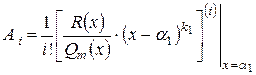 , … , …
| ||||||||||||
| Интегрирование простейших дробей | ||||||||||||
| тип | вид | замена | вычисление | |||||||||
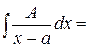
| 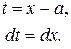
| 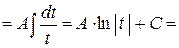
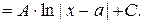
| ||||||||||
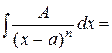
| 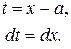
| 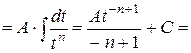
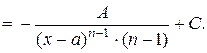
| ||||||||||
| 3а) | 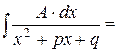
| выделяем квадрат трехчлена знаменателя
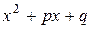 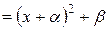
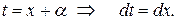
| 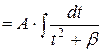 – табличный интеграл (см. 16 или 19). – табличный интеграл (см. 16 или 19).
| |||||||||
| 3b) | 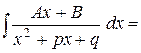
| выделить квадрат трехчлена знаменателя
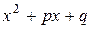 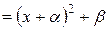
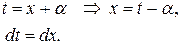
| 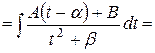 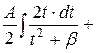
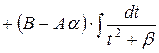 .
1-ый интеграл: .
1-ый интеграл: 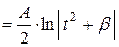 ,
2-ой – табличный интеграл
(см. 16 или 19). ,
2-ой – табличный интеграл
(см. 16 или 19).
| |||||||||
| 4а) | 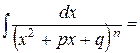
| выделить квадрат трехчлена знаменателя
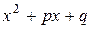 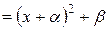
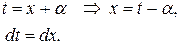
| 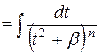 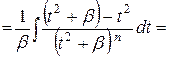
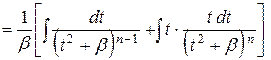 2-ой интеграл интегрируем по частям, где
2-ой интеграл интегрируем по частям, где 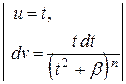 , он сведется к виду 1-ого, имеющего степень на единицу меньше. Повторяя процесс, приходим к табличному интегралу: 3а) или 3b). , он сведется к виду 1-ого, имеющего степень на единицу меньше. Повторяя процесс, приходим к табличному интегралу: 3а) или 3b).
| |||||||||
| 4b) | 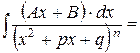
| выделить квадрат трехчлена знаменателя
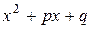 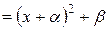
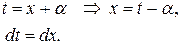
| 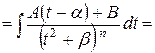 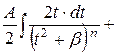
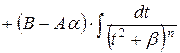 1-ый интеграл:
1-ый интеграл: 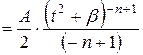 ,
2-ой – см. тип 4а). ,
2-ой – см. тип 4а).
| |||||||||
| Интегрирование тригонометрических выражений | ||||||||||||
| вид | замена | частные случаи | ||||||||||
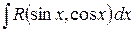
| Универсальная замена:
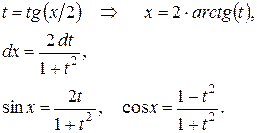
| |||||||||||
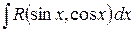
| 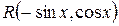 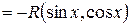 , т.е.
функция нечетная относительно , т.е.
функция нечетная относительно 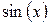 ,
то ,
то 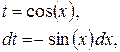 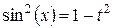 . .
| 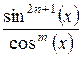 , ,
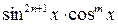 . .
| ||||||||||
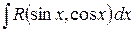
| 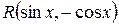 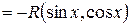 , т.е.
функция нечетная относительно , т.е.
функция нечетная относительно 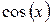 ,
то ,
то 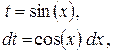 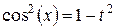 . .
| 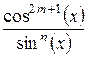 , ,
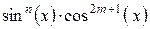 . .
| ||||||||||
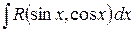
| 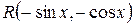 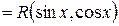 функция четная одновременно относительно функция четная одновременно относительно 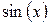 и и 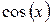 , то , то
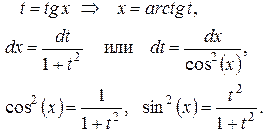
| |||||||||||
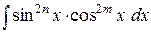
| Использовать формулы:
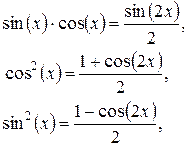
| |||||||||||
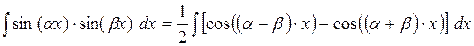 . .
| ||||||||||||
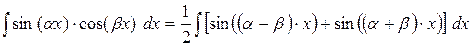 . .
| ||||||||||||
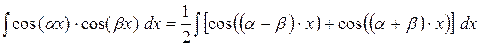 . .
| ||||||||||||
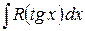
| 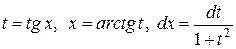 . .
| |||||||||||
| Интегрирование иррациональных выражений | ||||||||||||
| вид | замена | |||||||||||
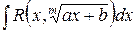
| 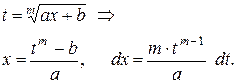
| |||||||||||
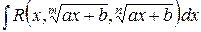
| 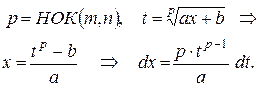
| |||||||||||
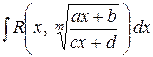
| 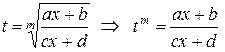 ,
решаем последнее уравнение и находим ,
решаем последнее уравнение и находим
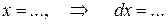
| |||||||||||
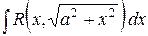
| 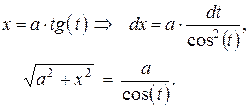
| |||||||||||
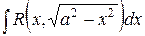
| 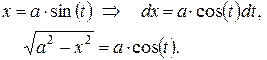
| |||||||||||
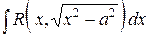
| 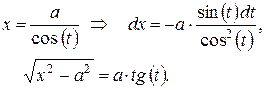
| |||||||||||
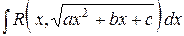
| выделяем полный квадрат трехчлена и приходим к одному из случаев № 4, 5, 6. | |||||||||||
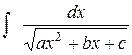
| выделяем полный квадрат трехчлена и получаем табличный интеграл (см. 18 или 20) | |||||||||||
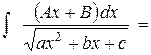
| 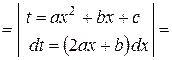 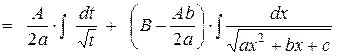 1-ый интеграл – табличный (см. 3), 2-ой – см. № 8.
1-ый интеграл – табличный (см. 3), 2-ой – см. № 8.
| |||||||||||
Приложения определенного интеграла
| Площадь плоской фигуры | |||
| в декартовых координатах | 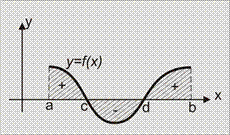 Фигура ограничена графиком функции Фигура ограничена графиком функции 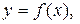 линиями линиями 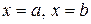 и осью и осью 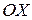
| 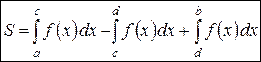
| |
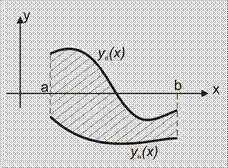 Фигура ограничена графиками функций Фигура ограничена графиками функций 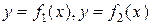 линиями линиями 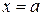 , , 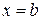
| 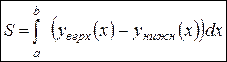 или
или
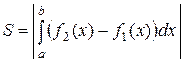
| ||
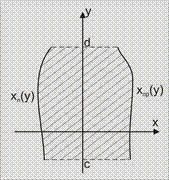 Фигура ограничена графиком функции Фигура ограничена графиком функции 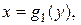 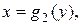 линиями линиями 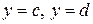 . .
| 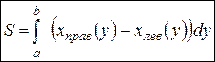 или
или
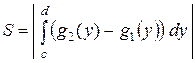
| ||
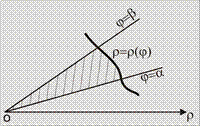
| в полярных координатах | Фигура ограничена графиком функции 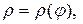 лучами лучами 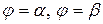
| 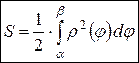
| |
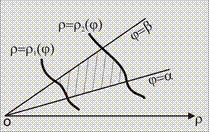 Фигура ограничена графиками функций Фигура ограничена графиками функций 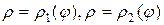 и лучами и лучами 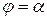 , , 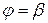
| 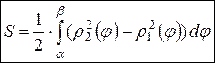
| ||
| Длина кривой в декартовых координатах | Дуга определяется графиком функции
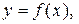 где где 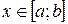
| 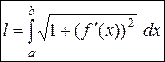
| |
| Длина кривой заданной параметрически | Дуга определяется графиком функции
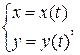 где где 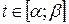
| 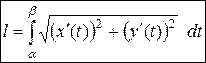
| |
| Длина кривой в полярных координатах | Дуга определяется графиком функции
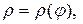 где где 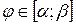
| 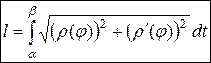
| |
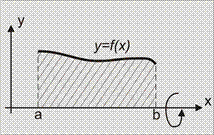
| Площадь поверхности тела вращения | Тело образовано вращением графика функции 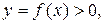 вокруг оси OX, ограниченного вокруг оси OX, ограниченного 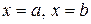
| 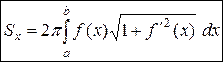
| |
| Объём тела вращения | 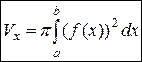
| ||
Тело образовано вращением графика функции 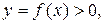 вокруг оси OY, ограниченного прямыми вокруг оси OY, ограниченного прямыми 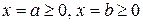
| 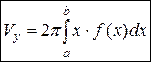
| ||
| Площадь поверхности тела вращения | 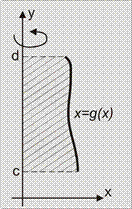 Тело образовано вращением графика функции Тело образовано вращением графика функции 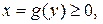 вокруг оси OY, ограниченного прямыми
вокруг оси OY, ограниченного прямыми 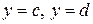
| 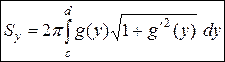
| |
| Объём тела вращения | 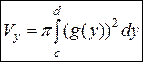
| ||
Тело образовано вращением графика функции 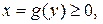 вокруг оси OX, ограниченного вокруг оси OX, ограниченного 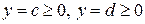
| 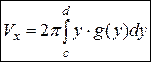
| ||
 2015-07-14
2015-07-14 344
344







