Типовой расчет по теме ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ
Пусть в некотором промежутке 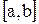 задана непрерывная функция
задана непрерывная функция 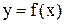 .
. 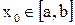 - заданная точка (рис.33).
- заданная точка (рис.33).
| |||
 | |||
У Д
В
Е
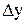
А 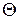
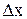 С
С
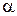
О а 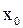
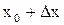 в х
в х
Рис. 1
отношения, когда 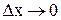 , называется производнойфункции
, называется производнойфункции 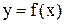 в заданной точке
в заданной точке 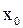 . Таким образом,
. Таким образом, 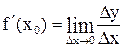 .
.
Замечание. Если 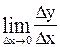 не существует, то и производной
не существует, то и производной 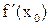 тоже не существует.
тоже не существует.
Производную функции 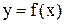 в произвольной точке х принято обозначать
в произвольной точке х принято обозначать 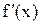 или
или 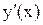 , или
, или 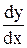 . Если же точка
. Если же точка 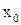 задана, значение производной в этой точке записывают в виде
задана, значение производной в этой точке записывают в виде 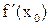 ,
, 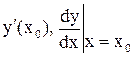 .
.
Производная функции в заданной точке характеризует скорость изменения функции в этой точке. Например, производная от пути по времени есть скорость движения, то есть 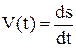 ; производная от скорости по времени дает ускорение движения
; производная от скорости по времени дает ускорение движения 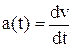 . Если функция
. Если функция 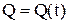 выражает количество электричества,
выражает количество электричества,
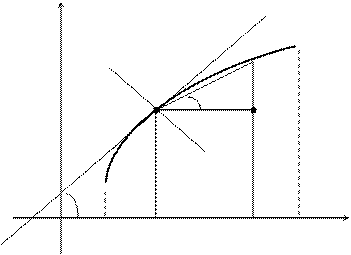
протекающего за время t через сечение проводника, то 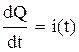 есть сила тока в момент времени t. Видно (рис. 33), что
есть сила тока в момент времени t. Видно (рис. 33), что 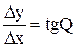 . Переходя к пределу при
. Переходя к пределу при 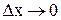 ,получаем
,получаем 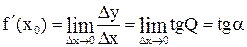 . Итак, производная функции в заданной точке равна тангенсу угла
. Итак, производная функции в заданной точке равна тангенсу угла 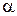 , который образует касательная в точке
, который образует касательная в точке 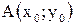 с осью ОХ:
с осью ОХ: 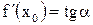 . Так как
. Так как 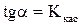 , то
, то 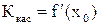 . Поскольку уравнение прямой с угловым коэффициентом имеет вид
. Поскольку уравнение прямой с угловым коэффициентом имеет вид 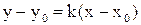 , то получим уравнение касательной АД:
, то получим уравнение касательной АД: 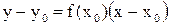 (рис. 33).
(рис. 33).
Так как нормаль 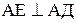 , то
, то 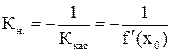 . Поэтому уравнение нормали АЕ имеет вид
. Поэтому уравнение нормали АЕ имеет вид 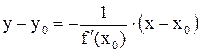 (рис. 33).
(рис. 33).
Пример. Найти производную функции 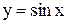 в производной точке х.
в производной точке х.
Решение. 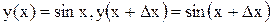 , тогда
, тогда 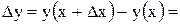
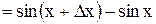 . Так как
. Так как 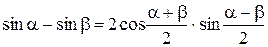 , то
, то
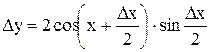 .
. 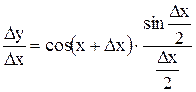 .
.
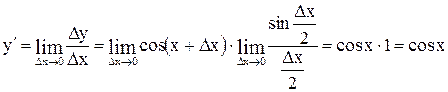 .
.
Замечание. При нахождении предела следует помнить, что 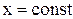 ,
, 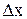 -переменная.
-переменная.
 2015-07-14
2015-07-14 297
297
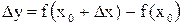 , это величина отрезка ВС (рис.1).
Отношение
, это величина отрезка ВС (рис.1).
Отношение 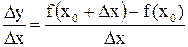 называется средней скоростью изменения фун-кции
называется средней скоростью изменения фун-кции 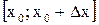 , а предел этого
, а предел этого







