Схема обробки експериментальних даних залежить від того, як проводились досліди: з повторенням чи без повторення. Якщо досліди проводились з повторенням, то схема обробки результатів виглядає так:
1. Знаходження коефіцієнтів рівняння регресії.
2. Оцінка дисперсій у кожному рядку таблиці.
3. Перевірка однорідності дисперсій.
4. Розрахунок дисперсії відтворення.
5. Перевірка значимості коефіцієнтів регресії.
6. Перевірка адекватності моделі.
Якщо досліди проводились без повторень по одному разу, то схема обробки результатів буде такою:
1. Знаходження коефіцієнтів моделі.
2. Знаходження дисперсії відтворення.
3. Перевірка значимості коефіцієнтів.
4. Перевірка адекватності моделі.
Знаходження коефіцієнтів рівняння регресії для першої схеми проводиться за середніми значеннями параметра оптимізації в кожному вектор-рядку, тобто
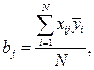
де 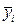 - середнє значення параметра оптимізації в і -му вектор-рядку; і =1; 2,...; N - кількість вектор-рядків; j =1, 2,...; k - кількість факторів.
- середнє значення параметра оптимізації в і -му вектор-рядку; і =1; 2,...; N - кількість вектор-рядків; j =1, 2,...; k - кількість факторів.
У випадку другої схеми коефіцієнти моделі обчислюють за формулою:
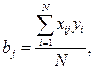
де позначки ті самі, що і раніше.
Знаходження дисперсії параметра оптимізації. Для обчислення похибки експерименту потрібна дисперсія параметра оптимізації або дисперсія відтворення. Цю величину знаходять на підставі значень повторних дослідів. Якщо в кожному вектор-рядку матриці планування здійснювалась однакова кількість повторних дослідів, то дисперсія параметра оптимізації знаходиться таким чином. Для кожного вектор-рядка матриці планування обчислюють дисперсію досліду:
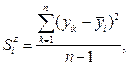
де і =1, 2,...; N - номери вектор-рядків; k= 1, 2,...; n - кількість повторних дослідів у кожному вектор-рядку; 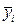 - середнє значення параметра оптимізації в кожному вектор-рядку.
- середнє значення параметра оптимізації в кожному вектор-рядку.
Після цього перевіряють однорідність одержаних дисперсій, тобто потрібно впевнитись, то всі групи експериментальних даних одержані з однієї і тієї самої сукупності і дають однакове розсіювання.
Для випадку, коли кількість повторних дослідів у кожному век
тор-рядку однакова, однорідність дисперсій перевіряють критерієм
Кохрена, який є відношенням максимальної дисперсії до суми всіх
дисперсій, тобто
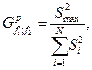
де f 1= n -1; f 2= N - числа ступеней вільності.
Якщо розраховане значення критерію Кохрена не перевищує табличного G T (дод. 5), тобто 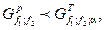 для заданого рівня значущості (як правило, a=0,05), то дисперсії є однорідними і їх можна усереднювати. Тоді дисперсія параметра оптимізації
для заданого рівня значущості (як правило, a=0,05), то дисперсії є однорідними і їх можна усереднювати. Тоді дисперсія параметра оптимізації
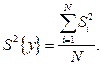
Число ступенів вільності цієї дисперсії f 1= N (n -1).
У випадку, коли кількість повторних дослідів у кожному вектор-рядку різна, то однорідність дисперсій перевіряють за критерієм Фішера або Бартлетта. У випадку використання критерію Фішера з усіх дисперсій вибирають найбільшу 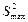 найменшу
найменшу 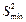 і обчислюють критерій Фішера як відношення
і обчислюють критерій Фішера як відношення
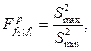
де f 1 - число ступенів вільності знаменника; f 2 - число ступенів вільності чисельника.
Якщо розраховане значення критерію Фішера не перевищує табличного, взятого при тих самих числах ступенів вільності, що і розраховане значення, і для заданого рівня значущості a (дод.7), то порівнювальні дисперсії є однорідними, тобто повинна виконуватись нерівність
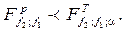
Коли найбільша та найменша дисперсії однорідні, то дисперсії, які мають проміжні значення, також будуть однорідними. Тоді дисперсія параметра оптимізації визначається за формулою
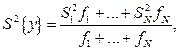
де 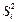 - дисперсії в кожному вектор-рядку; fi - числа ступенів вільності, з якими знаходились дисперсії у кожному вектор-рядку.
- дисперсії в кожному вектор-рядку; fi - числа ступенів вільності, з якими знаходились дисперсії у кожному вектор-рядку.
Однорідність дисперсій за критерієм Барлетта перевіряють таким чином. Спочатку обчислюють дисперсію параметра оптимізації:
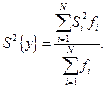
Далі знаходять розрахункове значення c2 - розподілу:
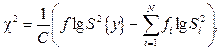
де
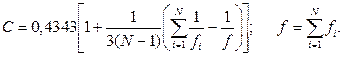
Тут число ступенів вільності дорівнює N -1, де N - кількість вектор-рядків у матриці планування.
Бартлеттом було показано, що величина
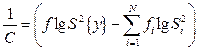
приблизно підпорядковується c2 - розподілу з (N -1) ступенями вільності. Тому розрахункове значення 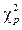 називають критерієм Бартлетта. Значимість критерію Бартлетта перевіряють звичайним способом, тобто шляхом порівняння розрахункового
називають критерієм Бартлетта. Значимість критерію Бартлетта перевіряють звичайним способом, тобто шляхом порівняння розрахункового 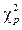 значення з табличним (дод. 8), взятим при тому самому ступені вільності (N -1) і заданому рівні значущості a. Якщо виконується нерівність
значення з табличним (дод. 8), взятим при тому самому ступені вільності (N -1) і заданому рівні значущості a. Якщо виконується нерівність 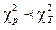 , то окремі дисперсії, що входять до дисперсії параметра оптимізації, є однорідними.
, то окремі дисперсії, що входять до дисперсії параметра оптимізації, є однорідними.
Наприклад, в чотирьох експериментах з нерівною кількістю повторних дослідів одержані результати, які наведені в табл. 14.
Таблиця 14
Вихідні дані для обчислення критерію Бартлетта
| Номер досліду |  | fi | Номер досліду |  | fi |
| 3,50 | 5,88 | ||||
| 4,22 | 22,36 |
За даними табл.. 14 одержимо
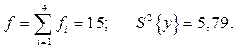
Тепер знайдемо величину С та 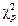 :
:

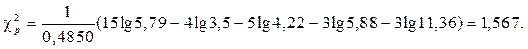
Табличне значення 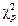 - розподілу (дод. 8) для трьох ступенів вільності і рівня значущості a=0,05 дорівнює 7,815. Оскільки розрахункове значення менше за табличне, то дисперсії однорідні.
- розподілу (дод. 8) для трьох ступенів вільності і рівня значущості a=0,05 дорівнює 7,815. Оскільки розрахункове значення менше за табличне, то дисперсії однорідні.
У зв’язку з тим, що плани першого порядку є рентабельними (S 2=const), то дублювати всі досліди в матриці планування потреби немає. Дублювання дослідів різко збільшує тривалість дослідження і витрати на його проведення, особливо за великої кількості вектор-рядків у матриці планування. В таких випадках або дублюють будь-який дослід у матриці планування, або проводять повторні досліди на нульовому рівні. Тоді дисперсія параметра оптимізації обчислюється за формулою
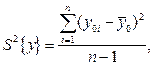
де n - кількість повторних дослідів; y 0 i - значення параметра оптимізації, які одержані на основному рівні в повторних дослідах; 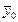 - середнє значення параметра оптимізації, яке обчислене за результатами повторних дослідів на основному рівні.
- середнє значення параметра оптимізації, яке обчислене за результатами повторних дослідів на основному рівні.
Число ступенів вільності цієї дисперсії f 1= n -1.
Ми розглянули випадки обчислення дисперсії параметра оптимізації, коли гіпотеза про однорідність дисперсій дослідів правильна. У таких випадках, коли дисперсії є неоднорідними змінюють масштаб для параметра оптипізації: вводиться деяка математична функція від параметра оптимізації, наприклад, квадратний корінь або логарифм.
Перевірка значущості коефіцієнтів регресі. Перевірку значущості коефіцієнтів рівняння регресії можна здійснювати двома рівноцінними способами: 1) побудовою довірчого інтервалу; 2) по обчисленню критерію Стьюдента.
При використанні повного або дробового факторного експерименту довірчі інтервали для усіх коефіцієнтів (в тому числі і для ефектів взаємодії) рівні між собою.
Для знаходження довірчого інтервалу необхідно перш аа все знайти дисперсію коефіцієнтів регресії 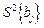 .
.
Для випадку, коли досліди в матриці планування повторювались, дисперсія коефіцієнтів рівняння регресії буде обчислена за формулою
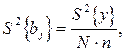
де 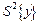 - дисперсія параметра оптимізації; N - кількість вектор-рядків у матриці планування; n - кількість повторних дослідів у вектор-рядках.
- дисперсія параметра оптимізації; N - кількість вектор-рядків у матриці планування; n - кількість повторних дослідів у вектор-рядках.
Якщо досліди у матриці планування не повторювались, а виконувались повторні досліди на основному рівні, то
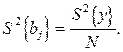
а довірчий інтервал (D b j) знаходиться за формулою
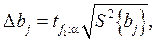
де 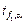 - табличне значення критерію Стьюдента, яке взято для числа ступенів вільності f 1, за якими знаходилась дисперсія параметра оптимізації та рівня значущості a (див. дод. 2).
- табличне значення критерію Стьюдента, яке взято для числа ступенів вільності f 1, за якими знаходилась дисперсія параметра оптимізації та рівня значущості a (див. дод. 2).
Коефіцієнти рівняння регресії вважаються значимими, якщо їх абсолютне значення більше за довірчий інтервал, тобто 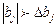 .
.
Для перевірки значущості коефіцієнтів по обчисленню t - критерію Стьюдента використовують формулу
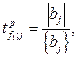
де 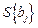 - середнє квадратичне відхилення коефіцієнта регресії, яке дорівнює кореню квадратному із дисперсії коефіцієнта регресії.
- середнє квадратичне відхилення коефіцієнта регресії, яке дорівнює кореню квадратному із дисперсії коефіцієнта регресії.
Обчислені значення t - критерію порівнюють з табличними при заданих a та f 1, Якщо виконується нерівність
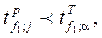
то коефіцієнт bj статистично значимий. За цією методикою значимість кожного коефіцієнта перевіряють окремо. Після перевірки значущості коефіцієнтів bj до рівняння регресії включають тільки ті коефіцієнти, які є значимими, а всі незначні коефіцієнти відкидають. Одержане таким чином рівняння регресії перевіряють на адекватність.
3.11.3. Перевірка адекватності моделі. Для перевірки гіпотези про адекватність моделі використовують критерій Фішера, розрахункове значення якого знаходять за формулою
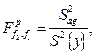
де 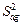 - дисперсія адекватності;
- дисперсія адекватності; 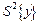 - дисперсія параметра оптимізації; f 1 - та f 2 - числа ступенів вільності, за якими знаходились дисперсія параметра оптимізації та дисперсія адекватності, відповідно.
- дисперсія параметра оптимізації; f 1 - та f 2 - числа ступенів вільності, за якими знаходились дисперсія параметра оптимізації та дисперсія адекватності, відповідно.
Розрахункове значення критерію Фішера порівнюють з табличним (дод. 7); взятим при тих самих ступенях вільності, та вибраному рівні значущості a, Якщо виконується нерівність
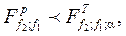
то модель адекватно описує реальну поверхню відгуку.
Таким чином, для перевірки адекватності моделі потрібно знайти дисперсіє адекватності, яка являє собою суму квадратів відхилень експериментальних та обчислених за допомогою рівняння регресії значень параметра оптимізації, поділеної на число ступенів вільності.
Якщо досліди в матриці планування виконувались з повтореннями, то дисперсію адекватності обчислюють за формулою:
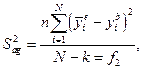
де n - кількість повторних дослідів в кожному вектор-рядку; N - кількість вектор-рядків у матриці планування; k - кількість статистично значимих коефіцієнтів (включаючи і b 0); f 2 - число ступенів вільності; 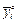 - середнє експериментальне значення параметра оптимізації в кожному вектор-рядку;
- середнє експериментальне значення параметра оптимізації в кожному вектор-рядку; 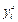 - обчисленне значення параметра оптимізації в і - му вектор-рядку.
- обчисленне значення параметра оптимізації в і - му вектор-рядку.
Якщо досліди в матриці планування проводились без повторень, то дисперсію адекватності обчислюють так:
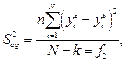
Наприклад, в результаті реалізації плану експерименту 22 були одержані результати, які наведені в табл. 15.
Таблиця 15
Матриця планування 22та результати експерименту
| Номер досліду | х 0 | х 1 | х 2 | х 1 х 2 | 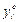 | 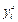 |
| + | - | - | + | 35,5 | ||
| + | - | + | - | 59,5 | ||
| + | + | + | + | 94,5 | ||
| + | + | - | - | 70,5 |
При цьому одержано таке рівняння регресії:
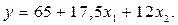
Тому розрахункові значення параметра оптимізації для кожного вектор-рядка будуть такими:
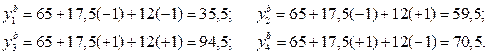
Тоді дисперсія адекватності
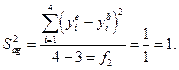
Наведені вище формули для дисперсії адекватності прийнятні лише для ненасичених планів, тобто для планів, у яких кількість значущих коефіцієнтів менша за кількість вектор-рядків у матриці планування. Для насичених планів адекватність лінійної моделі перевіряється за допомогою нуль-гіпотези. Її зміст полягає в тому, що для лінійної моделі сума усіх коефіцієнтів регресії å bij при квадратичних членах 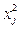 повинна дорівнювати нулю.
повинна дорівнювати нулю.
Цей метод оцінки оснований на тому, що вільний член лінійного
рівняння b 0 є сумісною оцінкою:
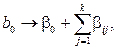
оскільки всі елементи стовпців x 0 та 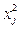 дорівнюють +1. Якщо ефекти при квадратичних членах відсутні, то
дорівнюють +1. Якщо ефекти при квадратичних членах відсутні, то 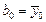 , де
, де 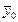 - середнє значення параметра оптимізації на основному рівні. Це дозволяє використовувати різницю
- середнє значення параметра оптимізації на основному рівні. Це дозволяє використовувати різницю
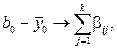
для орієнтовної характеристики кривизни поверхні відгуку { у } у вибраній частині факторного простору. Тому для перевірки нуль-гіпртези проводять додаткові досліди на нульовому рівні та за їх результатами обчислюють значення критерію Стьюдента:
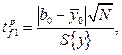
де N - кількість вектор-рядків у матриці планування; 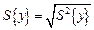 - середня квадратична похибка досліду; f 1= n -1 - число ступенів вільності, з якими знаходилась дисперсія параметра оптимізації
- середня квадратична похибка досліду; f 1= n -1 - число ступенів вільності, з якими знаходилась дисперсія параметра оптимізації 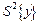 за «n» повторними дослідами на основному рівні.
за «n» повторними дослідами на основному рівні.
Якщо розрахункове значення критерію Стьюдента буде менше за табличне 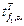 , взяте для того самого ступеня вільності і заданого рівня значущості a, то лінійна модель є адекватною, тобто для адекватної моделі повинна виконуватись нерівність
, взяте для того самого ступеня вільності і заданого рівня значущості a, то лінійна модель є адекватною, тобто для адекватної моделі повинна виконуватись нерівність 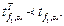 .
.
 2015-07-14
2015-07-14 1826
1826








