Лекция № 5. Элементы общей алгебры

РАЗДЕЛ II. ВВЕДЕНИЕ В ОБЩУЮ АЛГЕБРУ.

1. Свойства бинарных алгебраических операций.

Определение. На множестве А определена алгебраическая операция, если каждым двум элементам этого множества, взятым в определенном порядке, однозначным образом поставлен в соответствие некоторый третий элемент из этого же множества.

Примерами алгебраических операций могут служить такие операции как сложение и вычитание целых чисел, сложение и вычитание векторов, матриц, умножение квадратных матриц, векторное умножение векторов и др.

Отметим, что скалярное произведение векторов не может считаться алгебраической операцией, т.к. результатом скалярного произведения будет число, и числа не относятся к множеству векторов, к которому относятся сомножители.

Замечание. Вообще говоря, операция, определённая таким образом, называется бинарной, поскольку в ней участвуют два элемента. Но также можно говорить об унарных операциях, в которых участвует только один элемент данного множества, и в соответствие ему однозначным образом поставлен второй элемент этого множества. Таковы, например, операции извлечения корня квадратного или нахождения модуля числа.

Аналогично можно определить тринарную и прочие операции на данном множестве, в зависимости от количества участвующих в них элементов. В общем случае, 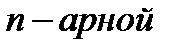операцией на множестве 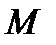будем называть функцию типа .

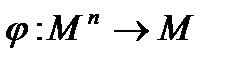Определение. Операция 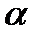, отображающая любой элемент множества 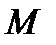в себя, называется тождественной операцией.

Тождественной операцией на множестве 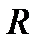, например, является умножение на единицу.

Для того чтобы описанные ниже соотношения выглядели бы более привычно, положим результат применения бинарной операции 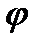элементам 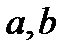записывать не в функциональном виде 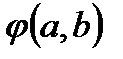, а виде 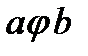, принятом для записи арифметических операций.

Определение. Операция 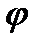называется коммутативной, если для любых элементов 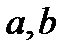выполняется: .

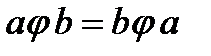Операции сложения и умножения чисел коммутативны, а вычитание и деление некоммутативны. Также некоммутативна операция умножения матриц (как известно из курса линейной алгебры).

Определение. Операция 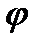называется ассоциативной, если для любых элементов 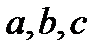выполняется: .

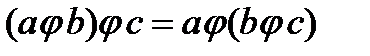Выполнение условия ассоциативности означает, что скобки в выражении 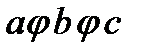можно не расставлять. Сложение и умножение чисел ассоциативны, что и позволяет не ставить скобки в выражениях типа 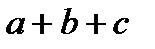и 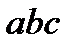. В качестве примера неассоциативной операции можно привести возведение в степень:

.

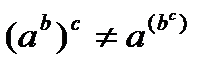Правда, запись 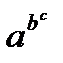является допустимой, но служит сокращением записи выражения 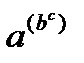, а не 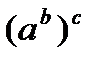(сокращённая запись которого - 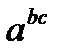). Важным примером ассоциативной операции является композиция отображений.

Определение. Операция 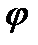называется дистрибутивной слева относительно операции 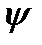, если для любых 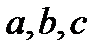выполняется:

,

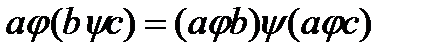и дистрибутивной справа относительно операции 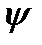, если для любых 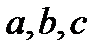выполняется:

.

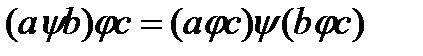Наличие свойства дистрибутивности позволяет раскрывать скобки. Например, умножение дистрибутивно относительно сложения (и вычитания) и справа, и слева:

.

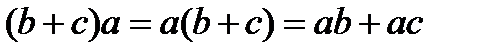Возведение в степень дистрибутивно относительно умножения справа: 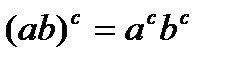, но не слева: 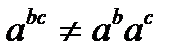. Сложение (и вычитание) чисел недистрибутивно относительно умножения: 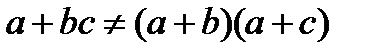. Ниже будет показано, что операции пересечения и объединения множеств дистрибутивны относительно друг друга и слева, и справа.

2. Алгебраические структуры.

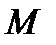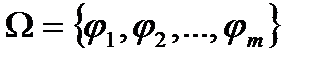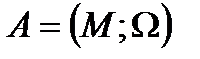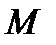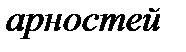Определение. Пусть дано некоторое множество , на котором задана совокупность операций . Структура вида называется алгеброй; множество называется несущим множеством, совокупность операций - сигнатурой, вектор “ ” операций 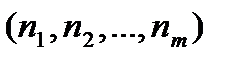называется типом.

Определение. Множество 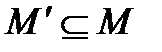называют замкнутым относительно 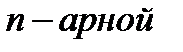операции 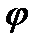на множестве 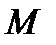, если значения функции 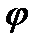на аргументах 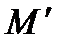принадлежат 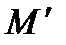(то есть 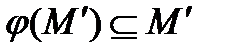). Если множество 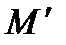замкнуто относительно всех операций 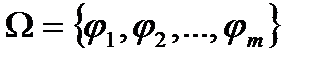, то структура 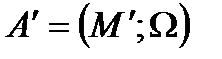называется подалгеброй алгебры .