Пример 2. “с точностью до изоморфизма”

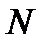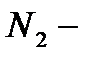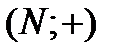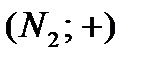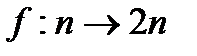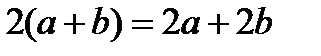а) Пусть - множество натуральных чисел, множество натуральных чётных чисел. Алгебры и изоморфны; изоморфизмом является отображение , причём условие здесь имеет вид . Поскольку 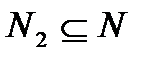, то данный изоморфизм есть изоморфизм алгебры 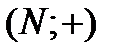в себя.

б) Изоморфизмом между алгебрам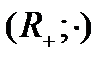и и 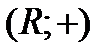является, например, отображение 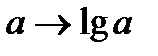. Условие имеет вид .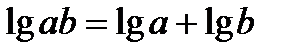

в) Булевы алгебры, образованные двумя различными множествами одинаковой мощности, изоморфны: операции у них просто одинаковы (см. выше), а отображением 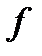может служить любое взаимнооднозначное соответствие.

Теорема 5.3. Отношение изоморфизма является отношением эквивалентности на множестве алгебр.

Понятие изоморфизма является одним из важнейших понятий в математике. Его сущность можно выразить следующим образом. Если две алгебры изоморфны, то элементы и операции любой из них можно переименовать таким образом, что эти алгебры совпадут. Это позволяет, получив некоторое эквивалентное соотношение в данной алгебре, распространять его на любую изоморфную ей алгебру. Распространённое в математике выражение “с точностью до изоморфизма” означает, что рассматриваются только те свойства объектов, которые сохраняются при изоморфизме, то есть являются общими для всех изоморфных объектов. В частности, изоморфизм сохраняет коммутативность, ассоциативность и дистрибутивность.