Явления несколько иного типа наблюдал в своих экспериментах Фраунгофер. Схема его экспериментов приведена ан рис А
Дифракция Фраунгофера от щели. Дифракция сферических или плоских волн на препятствии, расположенном на пути распространения света, и если дифракционная картина наблюдается на экране, расположенном на конечном расстоянии от препятствия, называется дифракцией Френеля (или дифракция в сходящихся лучах). Дифракция, при котором на препятствие падает плоская волна, а дифракционная картина наблюдается в фокальной плоскости собирающей линзы, установленной за препятствием, получила название дифракции Фраунгофера (или дифракция в параллельных лучах).
Пусть плоская монохроматическая световая волна падает нормально на непрозрачный экран (рис.6) с узкой щелью ширины а и длиной L>>а (т.е. щель бесконечно длинная). Дифракционная картина наблюдается на экране Э, находящейся в фокальной плоскости собирающей линзы.
Согласно принципу Гюйгенса-Френеля, каждя точка щели является источником вторичных волн, колеблющихся в одинаковой фазе, поскольку плоскость щели совпадает с фронтом падающей плоской волны.
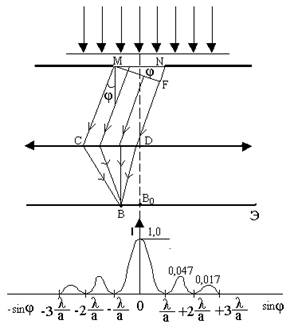
Параллельные пучки лучей, выходящие из щели в произвольном направлении φ (φ – σгол дифракции), собираются линзой в точке В. Открытую часть волновой поверхности MN в плоскости щели разбивают на зоны Френеля, имеющие вид полос и проведенных так, чтобы разность хода от их соответственных точек была равна λ/2. При этом на ширине щели уменьшается а*sin φ/(λ/2) ηон.
Все точки волнового фронта в плоскости щели колеблются в одинаковой фазе. Будут равны также амплитуды вторичных волн в плоскости щели (зоны Френеля одинаковы по площади и одинаково наклонены к направлению наблюдения). Следовательно, амплитуды, возбуждаемые в точке В соседними зонами, равны по амплитуде и противоположны по фазе.
Если число зон Френеля четное, т.е.
а*sinφ = ± 2*m*(λ/2) (m = 1,2,3,…), (14)
то в точке В наблюдается дифракционный минимум, если же число зон Френеля нечетное, т.е.
а*sinφ = ± (2m+1)*(λ/2) (m = 1,2,3,…), (15)
то наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля. В направлении φ = 0 наблюдается центральный дифракционный максимум.
Из условия (14) можно определить направления на точки экрана, где амплитуда (интенсивность, а она пропорциональна квадрату амплитуды) равна нулю, а из условия (15) – направления, где она максимальна. Следует, однако, заметить, что расчет с помощью зон Френеля является приближенным.
На рисунке 6 приведен дифракционный спектр – зависимость распределения интенсивности на экране от угла дифракции. основная часть световой энергии сосредоточена в центральном максимуме. С увеличением угла дифракции интенсивность побочных максимумов резко падает (относительная интенсивность максимумов I0:I1:I3… = 1:0,047:0,017…).
При освещении щели не монохроматическим, а белым светом центральный максимум имеет вид белой полоски (он общий для всех длин волн), боковые максимумы радужно окрашены (согласно (15), условие максимума при любых m различно для разных λ). Таким образом, справа и слева от центрального максимума наблюдаются максимумы первого и второго порядков, обращенных фиолетовым краем к центру дифракционной картины.
С уменьшением ширины щели центральный максимум расширяется (согласно (14), возрастают углы φ = ±arcsin(λ/a), κоторые соответствуют максимумам первого порядка, ограничивающим центральный максимум); при этом яркость его уменьшается. все сказанное относится и к другим максимумам.
С увеличением ширины щели (а > λ) дифракционные полосы становятся ỳже и ярче, а число полос больше. При а >> λ в центре получается резкое изображение источника света (прямолинейное распространение света).
При а = λ (что соответствует sinφ = 1 и φ = π/2) φентральный максимум расплывается в бесконечность и экран освещен равномерно.
Дифракция на двух и многих щелях. Дифракционная решетка. При дифракции Фраунгофера на щели распределение интенсивности на экране определяется направлением дифрагированных лучей. Поэтому перемещение щели параллельно самой себе не изменяет дифракционную картину. Следовательно, дифракционные картины, создаваемые двумя соседними щелями, будут одинаковыми. Результирующая картина определяется как результат взаимной интерференции волн, идущих от обеих щелей.
Пусть плоская монохроматическая волна падает нормально на непрозрачный экран (см. рис. 7) с двумя одинаковыми щелями шириной щели а, отстоящими друг от друга на расстоянии b (a + b =d). Очевидно, что минимумы будут на тех же местах, как и в случае одной щели, так как те направления, в которых ни одна из щелей н6е посылает света, не получит его и при двух щелях. Следовательно, прежние (главные) минимумы интенсивности наблюдаются в направлениях, определяемых условием (14):
a*sinφ = ± mλ (m=1,2,3,…). (16)
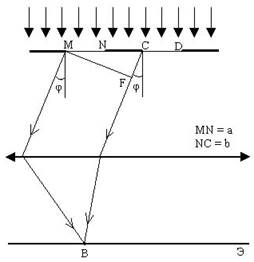 Вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях могут гасить друг друга, т.е. возникают дополнительные минимумы. Это будут направления, которым соответствует разность хода лучей кратное λ/2, посылаемых от соответственных точек обеих щелей (например, точек М и С). Такие направления будут определяться условием (см. рис.7):
Вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях могут гасить друг друга, т.е. возникают дополнительные минимумы. Это будут направления, которым соответствует разность хода лучей кратное λ/2, посылаемых от соответственных точек обеих щелей (например, точек М и С). Такие направления будут определяться условием (см. рис.7):
CM = MC sin φ = (a + b) sin φ = d sin φ = λ/2, 3λ/2,…. (17)
Таким образом, с учетом (17) условие дополнительных минимумов
d sin φ = ±(2 m+1)λ/2 (m = 1,2,3,…). (18)
В направлениях
d sin φ = ±2 mλ/2 = ± mλ (m = 1,2,3,…) (19)
действие одной щели усиливает действие другой, поэтому эти направления задают главные максимумы.
Таким образом, для двух щелей дифракционная картина определяется условиями:
главные минимумы а sin φ = λ, 2 λ, 3 λ, ….
дополнительные минимумы d sin φ = λ/2, 3λ/2, 5λ/2, …
главные максимумы d sin φ = 0, λ, 2 λ, 3 λ, …,
т.е. между двумя главными максимумами располагается дополнительный минимум, а максимумы становятся более узкими, чем в случае одной щели.
Аналогично можно показать, что между каждыми двумя главными максимумами (d sin φ = 0, λ, 2 λ, …) οри трех щелях располагается два дополнительных минимума (d sin φ = λ/3 θ 2λ/3, 4λ/3 θ 5λ/3,…), οри четырех щелях - три и т.д. В случае N щелей число дополнительных минимумов, наблюдаемых между соседними главными максимумами, составит N-1.
Систему параллельных щелей (штрихов)равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками, называют одномерной дифракционной решеткой. Суммарную ширину щели а и непрозрачного участка b между щелями называют постоянной решетки (d = a + b). Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной картине осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.
Главные минимумы при дифракции света на дифракционной решетке наблюдается при условии, соответствующем одной щели:
а sin φ = ± mλ (m = 1,2,3,…), (20)
главные максимумы – при условии:
d sin φ = ± nλ (n = 0,1,2,…), (21)
где n – порядок главных максимумов. Если какие-то значения φ удовлетворяют условиям (20) и (21), то главные максимумы, отвечающие этим направлениям не наблюдаются. например, при а=d/3 каждый третий максимум не наблюдается.
Между каждыми двумя главными максимумами находятся N-1 дополнительных минимумов, отвечающих условию
d sin φ = ± m′ λ/N (m ′ ≠ 1, N, 2N,…), (22)
т.е. m′ может принимать все целочисленные значения, кроме тех, при которых условие (22) в (21). Очевидно, что имеют место также N-2 дополнительных максимумов, интенсивность которых значительно меньше по сравнению с главными максимумами (самый сильный из наблюдаемых дополнительных максимумов составляет <5% от главного).
На рисунке 8 для примера приведена дифракционная картина, наблюдаемого для N = 4 и d/a = 3. В данном случае главные максимумы третьего, шестого и т.д. порядков приходятся на минимумы интенсивности от одной щели, в результате чего они не наблюдаются. Штриховая линия задает распределение интенсивности (обусловленное дифракцией на щели), умноженной на N2 (амплитуда колебаний от N щелей в N раз больше амплитуды посылаемой от одной щели, а Imax в N2 раз больше интенсивности, создаваемой в направлении φ одной щелью).
Чем больше число щелей, тем больше количество световой энергии проходит через решетку, тем больше минимумов образуется между двумя соседними максимумами, тем, следовательно, более интенсивным и более острыми будут максимумы. Максимальный порядок спектра, даваемого дифракционной решеткой, при нормальном падении света ограничивается условием │sin φ │≤ 1, поэтому, согласно (21),
nmax ≤ d/λ.
Следовательно, чтобы получить спектр хотя бы первого порядка, период решетки должен быть больше длины световой волны.
Положение главных максимумов зависит от длины световой волны (21). Поэтому при нормальном падении на решетку белого света все максимумы, кроме центрального разложатся в спектр, фиолетовая область которого обращена к центру дифракционной картины, красная – наружу.
При наклонном падении параллельного пучка света на дифракционную решетку разность хода сходственных лучей, показанных на рисунке (см. рис.9)
CB – AD = d sin φ0 - d sin φ = d(sin φ0 - sin φ),
где φ0 – угол падения пучка света на поверхность дифракционной решетки. Если d(sin φ0 - sin φ) равна целому числу длин волн, то наблюдаются максимумы. Следовательно, при наклонном падении света на дифракционную решетку условие главных максимумов
d(sin φ0 - sin φ) = ± nλ (n = 0,1,2,…),
 2015-07-21
2015-07-21 12144
12144