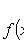
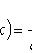
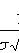
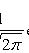
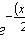
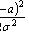
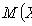
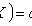
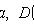
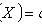
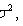
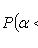
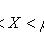
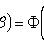
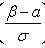
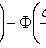
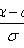
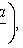
где 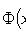
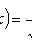
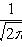
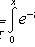
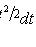 - функция Лапласа;
- функция Лапласа;
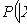
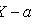
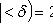
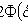
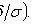
27
Вопрос № 21
Сочетание – это набор изmразличных элементов некоторого n-элементного множества, причем два любых сочетания, отличающиеся порядком следования элементов, совпадают. Стандартным обозначением для числа сочетаний mэлементов из n является символ 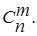 Число сочетаний вычисляется по формуле
Число сочетаний вычисляется по формуле 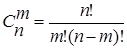 .
.
В задачах комбинаторики числа 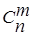 часто называют биномиальными коэффициентами. Это связано с тем, что они выступают в качестве коэффициентов в формуле бинома Ньютона
часто называют биномиальными коэффициентами. Это связано с тем, что они выступают в качестве коэффициентов в формуле бинома Ньютона


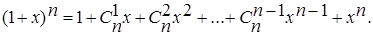
Между биномиальными коэффициентами имеется много важных и интересных соотношений. Например, 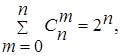
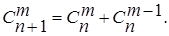 . Последнее тождество позволяет быстро вычислять биномиальные коэффициенты для небольших n по следующему правилу: для
. Последнее тождество позволяет быстро вычислять биномиальные коэффициенты для небольших n по следующему правилу: для 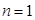
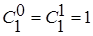 и формула позволяет перейти к
и формула позволяет перейти к 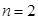 и т.д. Для использования этого алгоритма надо помнить, что
и т.д. Для использования этого алгоритма надо помнить, что 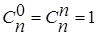 при любом n.
при любом n.
ВОПРОС № 22
Под схемой Бернулли понимают конечную серию 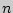 повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают
повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают 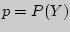 , а непоявления (неудачи) его
, а непоявления (неудачи) его 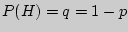 . Я. Бернулли установил, что вероятность ровно
. Я. Бернулли установил, что вероятность ровно 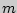 успехов в серии из
успехов в серии из 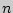 повторных независимых испытаний вычисляется по следующей формуле:
повторных независимых испытаний вычисляется по следующей формуле:
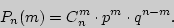
То значение 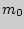 , при котором число
, при котором число 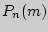 является максимальным из множества {
является максимальным из множества { 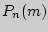 }, называется наивероятнейшим, и оно удовлетворяет условию
}, называется наивероятнейшим, и оно удовлетворяет условию
np - q 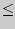 m
m 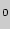
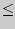 np+ p,
np+ p, 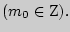
Формулу Бернулли можно обобщить на случай, когда при каждом испытании происходит одно и только одно из 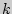 событий с вероятностью pi (i=1,2,…,k). Вероятность появления m1 раз первого события и m2
событий с вероятностью pi (i=1,2,…,k). Вероятность появления m1 раз первого события и m2 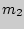 - второго и mk-k-го находится по формуле
- второго и mk-k-го находится по формуле
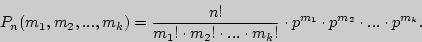
При достаточно большой серии испытаний формула Бернулли становится трудно применимой, и в этих случаях используют приближенные формулы. Одну из них можно получить из предельной теоремы Пуассона:
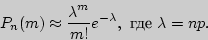
Таблица значений функции 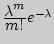 имеется в приложении 3.
имеется в приложении 3.
Вопрос № 24
Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Обозначается 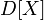 в русской литературе и
в русской литературе и 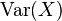 (англ. variance) в зарубежной. В статистике часто употребляется обозначение
(англ. variance) в зарубежной. В статистике часто употребляется обозначение 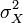 или
или 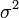 . Квадратный корень из дисперсии, равный
. Квадратный корень из дисперсии, равный 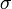 , называется среднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения.
, называется среднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения.
Из неравенства Чебышева следует, что случайная величина удаляется от её математического ожидания на более чем k стандартных отклонений с вероятностью менее 1/ k ². Так, например, как минимум в 75 % случаев случайная величина удалена от её среднего не более чем на два стандартных отклонения, а в примерно 89 % — не более чем на три.
Определение
Пусть 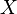 — случайная величина, определённая на некотором вероятностном пространстве. Тогда
— случайная величина, определённая на некотором вероятностном пространстве. Тогда
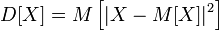
где символ 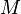 обозначает математическое ожидание[1][2].
обозначает математическое ожидание[1][2].
Замечания
· Если случайная величина 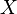 вещественна, то, в силу линейности математического ожидания, справедлива формула:
вещественна, то, в силу линейности математического ожидания, справедлива формула:
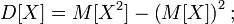
· Дисперсия является вторым центральным моментом случайной величины;
· Дисперсия может быть бесконечной. См., например, распределение Коши.
· Дисперсия может быть вычислена с помощью производящей функции моментов 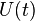 :
:
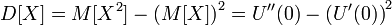
· Дисперсия целочисленной случайной величины может быть вычислена с помощью производящей функции последовательности.
Свойства
· Дисперсия любой случайной величины неотрицательна: 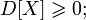
· Если дисперсия случайной величины конечна, то конечно и её математическое ожидание;
· Если случайная величина равна константе, то её дисперсия равна нулю: 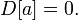 Верно и обратное: если
Верно и обратное: если 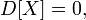 то
то 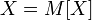 почти всюду;
почти всюду;
· Дисперсия суммы двух случайных величин равна:
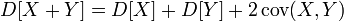 , где
, где 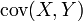 — их ковариация;
— их ковариация;
· Для дисперсии произвольной линейной комбинации нескольких случайных величин имеет место равенство:
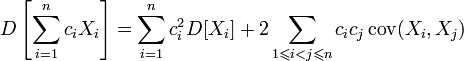 , где
, где 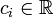 ;
;
· В частности, 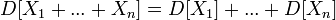 для любых независимых или некоррелированныхслучайных величин, так как их ковариации равны нулю;
для любых независимых или некоррелированныхслучайных величин, так как их ковариации равны нулю;
· 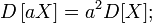
· 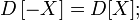
· 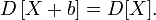
Пример
Пусть случайная величина 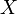 имеет стандартное непрерывное равномерное распределение на
имеет стандартное непрерывное равномерное распределение на 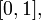 то есть её плотность вероятности задана равенством
то есть её плотность вероятности задана равенством
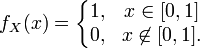
Тогда математическое ожидание квадрата случайной величины
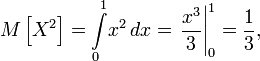
и математическое ожидание случайной величины
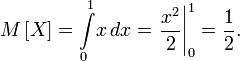
Тогда дисперсия случайной величины
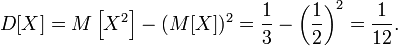
 2015-07-21
2015-07-21 282
282






