Однородные второго порядка 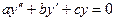 Составляется характеристическое уравнение:
Составляется характеристическое уравнение: 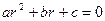 а) если дискриминант
а) если дискриминант 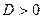 , то корни действительны и различны: , то корни действительны и различны: 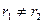 ,
то общее решение уравнения: ,
то общее решение уравнения: 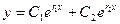 б) если
б) если 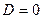 , то корень один , то корень один 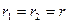 ,и общее решение: ,и общее решение: 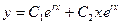 в) если
в) если 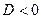 , то корни комплексные , то корни комплексные 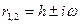 и решение: и решение: 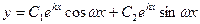
|
Однородные n -ого порядка 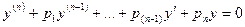
|
Составляется характеристическое уравнение: 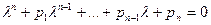 а)если корни действительны и различны:
а)если корни действительны и различны: 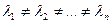 , то общее решение уравнения: , то общее решение уравнения:
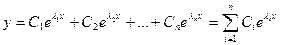 б)если среди корней характеристического уравнения имеются комплексные корни:
б)если среди корней характеристического уравнения имеются комплексные корни: 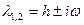 , то им соответствуют два линейно независимых решения: , то им соответствуют два линейно независимых решения: 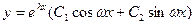 в)если среди корней характеристического уравнения имеется корень λ, кратности k > 1, то есть λ 1 = λ 2 = …= λ k = λ, тогда ему соответствуют k корней:
в)если среди корней характеристического уравнения имеется корень λ, кратности k > 1, то есть λ 1 = λ 2 = …= λ k = λ, тогда ему соответствуют k корней:
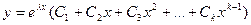 г)если
г)если 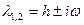 - комплексные корни, кратности k, то аналогично - комплексные корни, кратности k, то аналогично
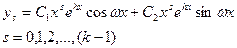
|
Неоднородные 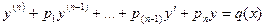
|
| Общее решение: у = уобщ + участн, где уобщ – это решение однородного уравнения, а участн находится методом вариации произвольных постоянных |
| Метод вариации произвольных постоянных а)если q(x) = eγxPm(x), где Pm(x) – многочлен m – ой степени, то частное решение нужно искать в виде: yчаст = xseγxQm(x), где Qm(x) – многочлен m – ой степени с неопределенными коэффициентами; s = 0, если γ – не является корнем характеристического уравнения s – равно кратности корня γ, если γ – является корнем характеристического уравнения б)если q(x) = eγx(Pn(x)cosβx + Rm(x)sinβx), где Pn(x) и Rm(x) многочлены степени m и п, тогда частное решение нужно искать в виде: yчаст = xseγx [Qk(x) cosβx + Dk(x)sinβx] где k = max{n;m} s = 0, если γ + iβ – не является корнем характеристического уравнения s – равно кратности корня γ, если γ +iβ – является корнем характеристического уравнения |
Решение линейных дифференциальных уравнений с постоянными коэффициентами
|
|

Сейчас читают про:
 2015-07-21
2015-07-21 293
293






