Краткое содержание лекции
Прямая в пространстве определяется в виде пересечения двух непараллельных и несовпадающих плоскостей
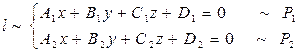 (1)
(1)
(1) называется общим уравнением прямой в пространстве.
Составить уравнение прямой, проходящей через точку 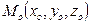 параллельно вектору
параллельно вектору 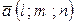 .
.
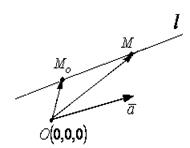
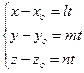 (2) – параметрическое уравнение прямой.
(2) – параметрическое уравнение прямой.
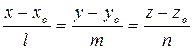 (3)
(3)
Пусть заданы прямые: L: 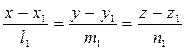 и
и
M: 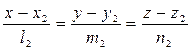 и
и
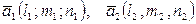 . Тогда:
. Тогда:
а) yгол между прямыми 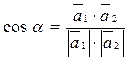 ;
;
б) условие параллельности 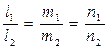 ;
;
в) условие перпендикулярности 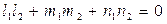 .
.
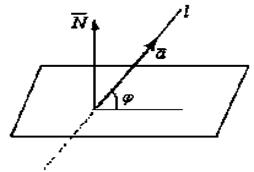
Угол между прямой и плоскостью
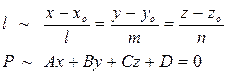 . Так как
. Так как 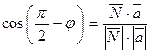 , то
, то 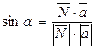 .
.
Задание на СРС
1. Линии второго порядка на плоскости. Реферат[1,3]
2. Решить задачи [2- стр. 279 №.2-4]
Задание на СРСП
1. Уравнение линии второго порядка в пространстве.[3,6]
Контрольные вопросы:
А. Для письменного контроля
1. Виды уравнения прямой в пространстве
2. условие параллельности и перпендикулярности прямых в пространстве
3. условие параллельности и перпендикулярности прямой и плоскости в пространстве
4. угол между прямыми
5. угол между прямой и плоскости
Б. Для компьютерного тестирования
1. Написать уравнение прямой, проходящей через точку 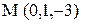 параллельно вектору
параллельно вектору 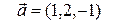 .
.
A) 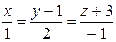 ; B)
; B) 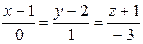 ; C)
; C) 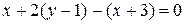 ;
;
D) 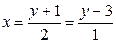 ; E)
; E) 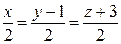
2. Составить каноническое уравнение прямой, проходящей через точки 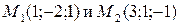
A) 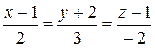 ; B)
; B) 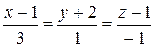 ; C)
; C) 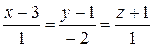 ;
;
D) 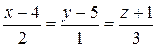 ; E)
; E) 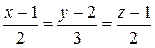 .
.
3 Найти точку пересечения плоскости 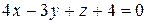 с осью
с осью 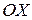 .
.
A) 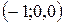 ; B)
; B) 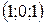 ; С)
; С) 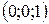 ; D)
; D) 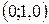 ; E)
; E) 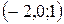
 2015-08-21
2015-08-21 242
242








