Пусть мы имеем функцию 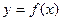 (1) определенную в некотором промежутке. При каждом значении аргумента
(1) определенную в некотором промежутке. При каждом значении аргумента 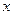 из этого промежутка функция
из этого промежутка функция 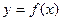 имеет определенное значение. Пусть аргумент
имеет определенное значение. Пусть аргумент 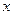 получил некоторое приращение
получил некоторое приращение 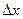 . Тогда функция
. Тогда функция 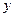 получит некоторое приращение
получит некоторое приращение 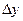 . Таким образом: при значении аргумента
. Таким образом: при значении аргумента 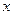 будем иметь
будем иметь 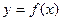 , при значении аргумента
, при значении аргумента 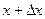 будем иметь
будем иметь 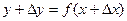 .
.
Найдем приращение функции 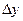 :
: 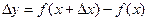 .
.
Составим отношение приращения функции к приращению аргумента: 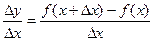 .
.
Найдем предел этого отношения при 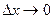 . Если этот предел существует, то его называют производной данной функции
. Если этот предел существует, то его называют производной данной функции 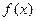 и обозначают
и обозначают 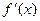 . Таким образом, по определению,
. Таким образом, по определению, 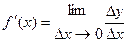 (2)
(2)
Операция нахождения производной от функции 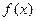 называется дифференцированием этой функции.
называется дифференцированием этой функции.
а) Механический смысл производной. Если зависимость расстояния 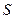 движущейся точки от времени
движущейся точки от времени 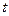 выражается формулой
выражается формулой 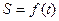 , то скорость
, то скорость 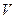 в момент
в момент 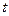 выражается формулой
выражается формулой 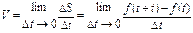 . Следовательно,
. Следовательно, 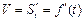 , (3) т.е. скорость равна производной от пути по времени
, (3) т.е. скорость равна производной от пути по времени 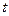 .
.
б) Геометрический смысл производной. Значение производной 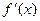 при данном Dy значении аргумента
при данном Dy значении аргумента 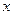 равняется тангенсу угла, a бразованного с положительным направлением оси
равняется тангенсу угла, a бразованного с положительным направлением оси 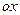 касательной к графику функции
касательной к графику функции 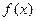 в соответствующей точке
в соответствующей точке 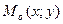 т.е.
т.е. 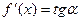 (4)
(4)
2. Дифференцируемость функции. Правила дифференцирования.
Определение. Если функция 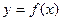 имеет производную в точке
имеет производную в точке 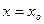 , т.е. если существует
, т.е. если существует 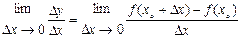 , то мы говорим, что при данном значении
, то мы говорим, что при данном значении 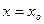 функция дифференцируема или имеет производную. Если функция дифференцируема в каждой точке некоторого отрезка
функция дифференцируема или имеет производную. Если функция дифференцируема в каждой точке некоторого отрезка 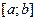 или интервала
или интервала 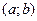 , то говорят, что она дифференцируема на отрезке
, то говорят, что она дифференцируема на отрезке 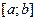 или, соответственно, в интервале
или, соответственно, в интервале 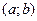 .
.
Теорема. Если функция 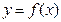 дифференцируема в некоторой точке
дифференцируема в некоторой точке 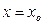 , то она в этой точке непрерывна. В точках разрыва функция не может иметь производной.
, то она в этой точке непрерывна. В точках разрыва функция не может иметь производной.
3. Производная обратной и сложной функции
а) Теорема. Если для функции 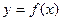 существует обратная функция
существует обратная функция 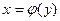 , которая в рассматриваемой точке
, которая в рассматриваемой точке 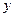 имеет производную
имеет производную 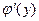 , отличную от нуля, то в соответствующей точке
, отличную от нуля, то в соответствующей точке 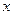 функция
функция 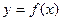 имеет производную
имеет производную 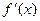 , равную
, равную 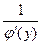 , т.е. справедлива формула
, т.е. справедлива формула 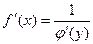 (5)
(5)
б) Производная от сложной функции. Пусть дана сложная функция 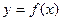 , т.е. такая, что ее можно представить в следующем виде:
, т.е. такая, что ее можно представить в следующем виде: 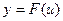 ,
, 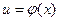 или
или 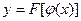 .
.
Теорема. Если функция 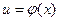 имеет в некоторой точке
имеет в некоторой точке 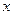 производную
производную 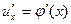 , а функция
, а функция 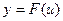 имеет при соответствующем значении и производную
имеет при соответствующем значении и производную 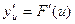 , тогда сложная функция
, тогда сложная функция 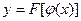 в указанной точке
в указанной точке 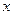 также имеет производную, которая равна
также имеет производную, которая равна
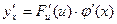 , (6)
, (6)
где в место и должно быть подставлено выражение 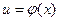 . Коротко,
. Коротко, 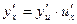 , т.е. производная сложной функции равна произведению производной данной функции по промежуточному аргументу и на производную промежуточного аргумента по
, т.е. производная сложной функции равна произведению производной данной функции по промежуточному аргументу и на производную промежуточного аргумента по 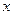 .
.
Пример. 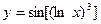 . Найти
. Найти 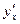
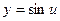 ,
, 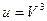 ,
, 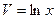 .
.
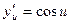 ,
, 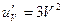 ,
, 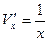 .
. 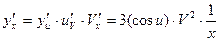 ,
,
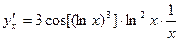 .
.
Задание на СРС:
1. Основные правила дифференцирования. Таблица дифференциалов.(конспект, по графику) [1,4-с.190-194]
2. Решить задачи - [2, стр. 291, №1-3; 3]
Задание на СРСП:
- Производные обратной тригонометрической функции.
- Вычисление производной от сложной функции. [4, с-186]
Контрольные вопросы:
А. Для письменного контроля
1. Определение производной функции. 2. Механический смысл производной.
3. Геометрический смысл производной. 4. Основные правила дифференцирования;
Б. Для компьютерного тестирования
Найти производные функции.
1) 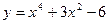 ; 2)
; 2) 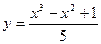 ; 3)
; 3) 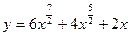 ; 4)
; 4) 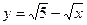
5) 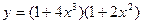 ; 6)
; 6) 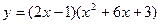 ; 7)
; 7) 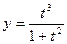 ; 8)
; 8) 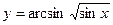
9) 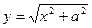 ; 10)
; 10) 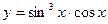 ; 11)
; 11) 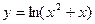 ; 12)
; 12) 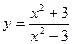 .
.
 2015-08-21
2015-08-21 172
172







