Теорема о пределе суммы (разности) членов числовых последовательностей
Если ч.п. 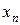 и
и 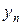 имеют пределы
имеют пределы
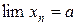 и
и 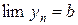 ,
,
то 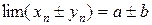 . Принимаем без доказательства.
. Принимаем без доказательства.
Теорема о пределе произведения членов числовых последовательностей
Если ч.п. 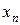 и
и 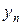 имеют пределы
имеют пределы
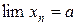 и
и 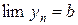 ,
,
то 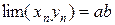 . Принимаем без доказательства. Следствием настоящей теоремы является утверждение о том, что постоянную можно вынести за знак предела.
. Принимаем без доказательства. Следствием настоящей теоремы является утверждение о том, что постоянную можно вынести за знак предела.
Теорема о пределе отношения членов числовых последовательностей
Если ч.п. 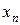 и
и 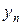 имеют пределы
имеют пределы
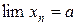 и
и 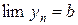 ,
,
причем 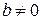 ,
,
то 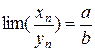 . Принимаем без доказательства.
. Принимаем без доказательства.
3. Бесконечно малые и бесконечно большие величины и их свойства
3.1. Бесконечно малые и бесконечно большие величины
Определение. Бесконечно малой называется ч.п. 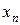 , предел которой равен 0
, предел которой равен 0
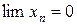 .
.
Для этого случая по любому положительного числа 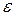 найдется номер
найдется номер 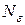 такой, что для любых
такой, что для любых 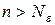 выполняется неравенство
выполняется неравенство
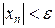 .
.
Очевидно, что если 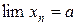 , то
, то 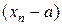 или
или 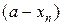 - будут бесконечно малыми величинами. И наоборот, если
- будут бесконечно малыми величинами. И наоборот, если 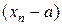 или
или 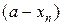 бесконечно малые величины, то
бесконечно малые величины, то 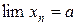 .
.
Определение. Ч.п. 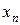 называется бесконечно большой, если для любого (сколь угодно большого) числа
называется бесконечно большой, если для любого (сколь угодно большого) числа 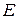 найдется номер
найдется номер 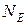 такой, что для любых
такой, что для любых 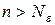 выполняется неравенство
выполняется неравенство
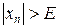 .
.
Если ч.п. сохраняет свой знак, то пишут 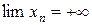 или
или 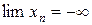 . Иногда вместо знака
. Иногда вместо знака 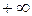 пишут знак
пишут знак 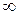 .
.
Пример. Ч. п. 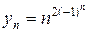 не является бесконечно большой величиной.
не является бесконечно большой величиной.
3.2. Связь бесконечно малых и бесконечно больших величин
Если ч.п. 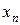 является бесконечно малой и нигде ее члены в ноль не обращаются, то очевидно ч.п.
является бесконечно малой и нигде ее члены в ноль не обращаются, то очевидно ч.п. 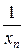 является бесконечно большой. И - наоборот.
является бесконечно большой. И - наоборот.
3.3. Типы неопределенных выражений
В случаях, когда теоремы о пределе суммы или разности, произведения или частного оказываются не применимыми, говорят о наличии неопределенности в выражении, стоящем под знаком предела. К ним относят следующие неопределенные выражения:
1. неопределенность типа 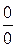 , когда вычисляется предел отношения
, когда вычисляется предел отношения 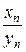 , в котором
, в котором 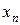 и
и 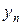 - бесконечно малые величины;
- бесконечно малые величины;
2. неопределенность типа 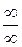 , когда вычисляется предел отношения
, когда вычисляется предел отношения 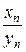 , в котором
, в котором 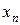 и
и 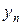 - бесконечно большие величины;
- бесконечно большие величины;
3. неопределенность типа 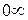 , когда вычисляется предел произведения
, когда вычисляется предел произведения 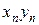 , в котором
, в котором 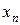 бесконечно малая а
бесконечно малая а 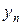 - бесконечно большая величина;
- бесконечно большая величина;
4. неопределенность типа 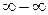 , когда вычисляется предел разности
, когда вычисляется предел разности 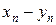 , в котором
, в котором 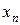 и
и 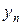 - бесконечно большие величины. Помимо них встречаются неопределенности типов
- бесконечно большие величины. Помимо них встречаются неопределенности типов 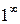 и
и 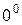 .
.
Для вычисления этих пределов применяют различные приемы раскрытия неопределенных выражений. В частности используют теорему о том, что если 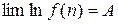 , то
, то 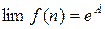 .
.
При вычислении пределов используют следующую классификацию б. м. величин.
Если 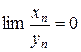 , то
, то 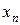 считают величиной более высокого порядка малости по сравнению с
считают величиной более высокого порядка малости по сравнению с 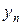 и пишут
и пишут 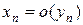 .
.
Если 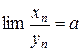 (
(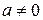 ), то величины
), то величины 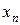 и
и 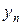 считают величинами одного порядка малости.
считают величинами одного порядка малости.
Если 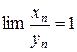 , то величины
, то величины 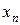 и
и 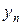 считают эквивалентными. Одну эквивалентную величину можно заменять на другую в произведениях и частном.
считают эквивалентными. Одну эквивалентную величину можно заменять на другую в произведениях и частном.
Аналогичным образом осуществляют сравнение бесконечно больших величин.
Для раскрытия неопределенных выражений типа 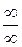 применяют теорему Штольца.
применяют теорему Штольца.
Теорема (Штольца). Пусть числовая последовательность 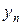 является возрастающей бесконечно большой величиной, а
является возрастающей бесконечно большой величиной, а 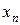 - бесконечно большая величина. Тогда выполняется соотношение
- бесконечно большая величина. Тогда выполняется соотношение
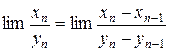 ,
,
если только существует предел справа (конечный или бесконечный).
В зависимости от сравниваемых числовых последовательностей 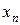 и
и 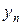 предел может быть конечным числом, нулем, или не существовать.
предел может быть конечным числом, нулем, или не существовать.
Примеры.
1. 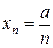 ,
, 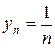 . Тогда
. Тогда 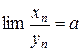 - конечное число.
- конечное число.
2. 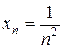 ,
, 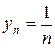 . Тогда
. Тогда 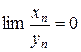 .
.
3. 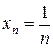 ,
, 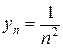 . Тогда
. Тогда 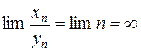 .
.
4. 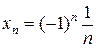 ,
, 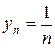 . Тогда
. Тогда 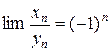 - не существует.
- не существует.
5. 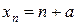 ,
, 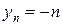 . Тогда
. Тогда 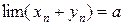 .
.
6. 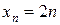 ,
, 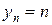 . Тогда
. Тогда 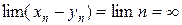 .
.
7. 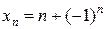 ,
, 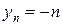 . Тогда
. Тогда 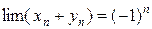 - не существует.
- не существует.
4. Число 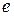
Особое место в математике занимает число 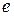 . Оно определяется как предел числовой последовательности
. Оно определяется как предел числовой последовательности
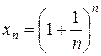 (1)
(1)
Для анализа характера изменения членов числовой последовательности воспользуемся формулой бинома Ньютона
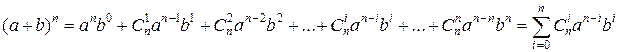 ,
,
(2)
где 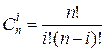 - число сочетаний из
- число сочетаний из 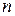 элементов по
элементов по 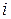 .
.
Применим формулу (2) к соотношению (1). В результате получим
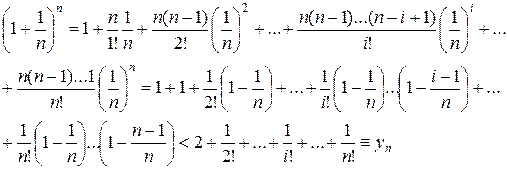 . (3)
. (3)
Таким образом, получено, что
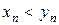 . (4)
. (4)
Оценим сверху члены числовой последовательности 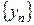
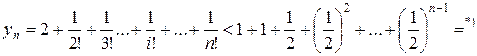 .
.
Последнее соотношение есть сумма членов геометрической прогрессии с первым членом 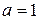 и знаменателем
и знаменателем 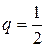 . Поэтому
. Поэтому
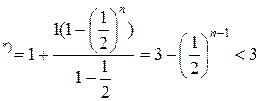 .
.
Итак, последовательность (1) ограничена сверху. Она является также возрастающей. Действительно, из формулы (3) видно, что для следующего члена последовательности число положительных слагаемых возрастет на единицу и каждое слагаемое, начиная с третьего увеличится. Возрастающая, ограниченная сверху последовательность имеет предел
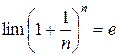 .
.
Для оценки числа 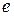 выполним следующие рассуждения. В (3) отбросим последние члены суммы
выполним следующие рассуждения. В (3) отбросим последние члены суммы
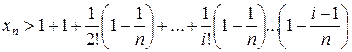 .
.
В последнем соотношении перейдем к пределу
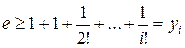 .
.
Заменяя в последнем соотношении индекс 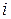 на
на 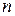 и с учетом неравенства (14) получаем
и с учетом неравенства (14) получаем
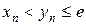 .
.
С учетом теоремы о сжатой переменной получаем важное соотношение
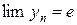 . (5)
. (5)
Именно оно позволяет вычислить число 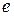 с любой заданной точностью. При этом пользуются следующим соотношением
с любой заданной точностью. При этом пользуются следующим соотношением
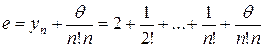 , (6)
, (6)
где 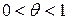 .
.
Число 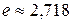 . Оно используется как основание натуральных логарифмов и записывается в виде
. Оно используется как основание натуральных логарифмов и записывается в виде
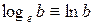 .
.
Известно, что формула перехода от основания 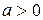 к основанию
к основанию 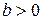 логарифмов имеет вид
логарифмов имеет вид
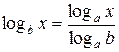 .
.
Если 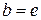 и
и 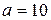 , получим
, получим
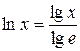 .
.
Если 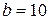 и
и 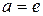 , получим
, получим
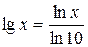 .
.
[1] B. Bolzano - чешский математик, A.L. Cauchy - французский математик
 2015-08-21
2015-08-21 1933
1933