Характерные особенности и общая постановка транспортной задачи

Характерными особенностями транспортных моделей являются: 1) наличие не менее двух исходных пунктов поставки; 2) наличие не менее двух конечных пунктов потребления; 3) из каждого исходного пункта в каждый конечный пункт поставляется однородная продукция – хлысты, сортименты, пиломатериалы и пр.; 4) известны или можно определить величины, характеризующие объем продукции, поставляемой из каждого исходного пункта, – мощность по отгрузке каждого исходного пункта; 5) известны или можно определить объемы продукции, потребляемые в каждом пункте назначения, – мощность по приемке каждого из пунктов потребления; 6) известны или можно определить себестоимость (затраты) или прибыль перевозки единицы продукции из каждого исходного пункта в каждый пункт потребления.

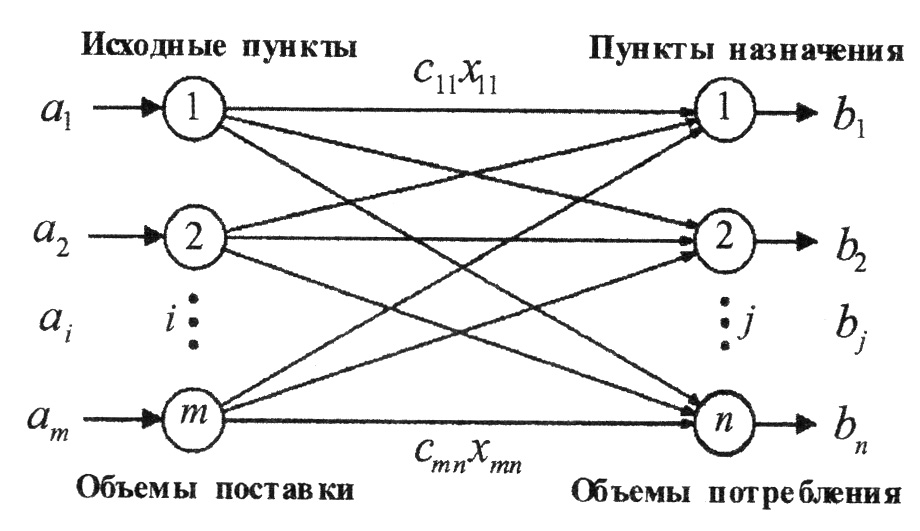
Цель, достигаемая решением транспортной задачи, – определение такого количества продукции, которое следует транспортировать из каждого исходного пункта в каждый пункт назначения и при котором транспортные расходы будут минимальными или прибыль (в линеаризованных задачах) от транспортировок будет максимальна. Какова цель – минимизация затрат на транспортировку или максимизация прибыли – таков и выбор критерия. На рис. 5.18 изображена транспортная модель в виде сети с т исходными пунктами и п пунктами назначения. Исходным пунктам и пунктам назначения соответствуют вершины (окружности), а маршрутам транспортировки – дуги (прямые линии). Количество продукции, отгружаемое (производимое) в каждом пункте i, обозначим через а_i, а потребляемое (хранимое) в каждом пункте j – через b_j; с_ij – себестоимость транспортировки единицы продукции из каждого исходного пункта i в каждый пункт назначения j.

Рис. 5.18. Схематическое представление транспортной модели

Обозначим через x_ij – количество продукции (объемы), перевозимое из исходного пункта i в пункт назначения j. Тогда задача ЛП транспортного типа в общем виде формулируется следующим образом:

минимизировать у= 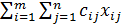(5-13)

при ограничениях 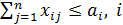= 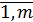(5.14)

весь объем транспортировки из каждого i -го пункта не может быть больше, чем там имеется в наличии:

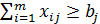, j = 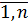; (5.15)

весь объем транспортировки в каждый j -й пункт должен быть, по крайней мере, равен спросу (потребности) этого пункта:

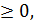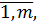x_ij i = j= 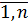. (5.16)

Если суммарный объем исходных пунктов (поставщиков) равен суммарному объему пунктов потребления (потребителей), Σ а_i =Σ b_j, то модель называется сбалансированной транспортной моделью.

В реальных производственных ситуациях не всегда соблюдается изложенное условие – объем поставок равен объему потребления. Поэтому с целью упрощения процесса решения транспортную модель искусственно приводят к сбалансированной посредством введения фиктивных исходных пунктов или фиктивных пунктов назначения. В этом случае в выражения ограничений (5.14) – при введении фиктивного исходного пункта – или (5.15) – при введении фиктивного пункта потребления – вносятся соответствующие дополнения. Стоимость транспортировки из фиктивного исходного в фиктивный пункты потребления принимается равной нулю.

ВЫБОР ОПТИМАЛЬНОГО ПЛАНА ТРЕЛЕВКИ

Здесь представлен пример постановки транспортной задачи [3] для ситуации, когда объемы поставки не равняются объемам потребления. Задачи такого типа весьма актуальны в текущий момент в связи истощенным лесным фондом и, как следствие, наличием отводимых в рубку разрозненных лесосек неправильной конфигурации. Постановку задачи для нашего примера рассмотрим в последовательности, рекомендуемой в разделах 1.1, 1.5, 2.3.

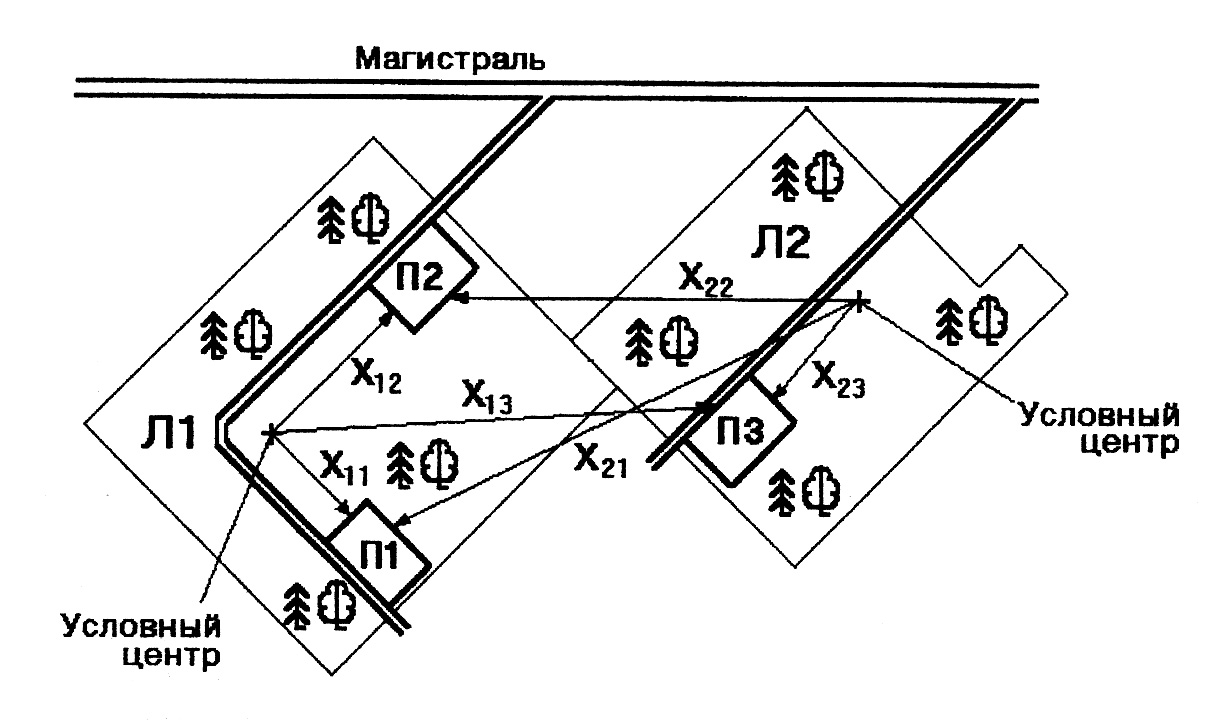
5.4.2.1. Содержание заданной ситуации. Имеются две лесосеки Л₁ и Л₂, в каждой из которых базируется по одной лесозаготовительной бригаде. Обе бригады производят трелевку хлыстов на три погрузочных пункта П₁, П₂ и П₃. Изложенная ситуация представлена на рис. 5.19. Сменный объем трелевки с лесосеки Л₁–Q₁=250 м³, с лесосеки Л₂–Q₂=150 м³.

Вместимость погрузочных пунктов в расчете на смену составляет, соот­ветственно, V ₁=200 м³; V ₂=150 м³; V₃ =100 м³. Себестоимость трелевки 1 м³ с каждой лесосеки на каждый погрузочный пункт составляет, соответственно: с первой на первый – 2 руб.; с первой на второй – 1,5 руб.; с первой на третий – 4 руб.; со второй на первый – 3 руб.; со второй на второй – 2 руб.; со второй на третий 1 руб. Для корректного решения рассматриваемой задачи введем допущение о том, что трелевка производится с условных центров лесосек. Перечисленные ранее затраты на трелевку 1 м³ являются средними по каждой лесосеке и определены трелевкой из условных центров.

Рис. 5.19. Графическое представление задачной ситуации

Необходимо определить такие объемы трелевки с каждой из лесосек на каждый погрузочный пункт, при которых суммарные затраты на трелевку были бы минимальны.

5.4.2.2. Постановка задачи выбора оптимального плана трелевки.

Определение цели. Найти объемы трелевки с каждой лесосеки на каждый погрузочный пункт, минимизирующие затраты на трелевку в смену (транспортные издержки).

Формулировка проблемы. Общая содержательная формулировка задачи дана в п. 5.4.2.1.

Этапы формулировки проблемы включают в себя:

1) управляемые переменные – сменные объемы трелевки с каждой лесосеки на каждый погрузочный пункт, м³;

2) переменные состояния – технологические и технико – экономические факторы: сменные объемы трелевки с каждой лесосеки, вместимости каждого погрузочного пункта, себестоимость трелевки 1 м³ с каждой лесосеки на каждый погрузочный пункт по соответствующим волокам, количество лесосек и погрузочных пунктов;

3) размерность задачи – определяется количеством управляемых переменных и ограничений с учетом несбалансированности, равняется девяти, временной интервал моделирования – смена;

4) критерий - суммарные затраты на трелевку, руб.

Построение математической модели. Для построения математической модели принимается допущение о том, что производится транспортировка однородной продукции и конструируемая транспортная модель является однопродуктовой. С порядком конструирования и решения многопродуктовых моделей можно познакомиться в [7 и 55].

Построение (конструирование) математической модели производится в следующем порядке:

1) обозначение переменных – объемов трелевки с каждой лесосеки в каждый погрузочный пункт – производится в соответствии с рис. 5.19 (в обозначениях первый индекс i соответствует номеру лесосеки, второй j – номеру погрузочного пункта) и имеет следующий вид: х ₁₁, x ₁₂, x ₁₃, x ₂₁, x ₂₂, x ₂₃; у – функция цели;

2) целевая функция разрабатывается исходя из того, что затраты на любой из маршрутов равны произведению себестоимости трелевки 1 м³ по данному маршруту на объем трелевки (пока неизвестный) лесоматериалов по этому же маршруту, отсюда и с учетом выражения (5.13) функция цели примет следующий вид:

у = 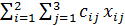=2 х ₁₁+1,5 x ₁₂+4 х ₁₃+З x ₂₁+2 х ₂₂+1 x ₂₃;

3) построение ограничений производится на основе содержательной сущ­ности задачи, в которой отражены: а) ограничения на объем трелевки с каждой лесосеки: необходимо стрелевать с каждой лесосеки столько древесины, сколько на них заготавливается в смену; б) ограничения на объем поступления или по­требления: необходимо доставить на каждый погрузочный пункт столько древе­сины, сколько обеспечивает его вместимость, и не менее. В содержании задачи определено, что суммарный объем трелевки в смену Q = Q ₁+ Q ₂=400 м³, а вме­стимость погрузочных пунктов V=V₁+V₂+V₃=450 м³. В этом случае имеем несбалансированную транспортную модель, Q<V. Приведение транспортной модели к сбалансированной, чтобы недостаток древесины в 50 м³ для погрузочных пунктов оптимально распределялся между ними, производится введением дополнительной фиктивной лесосеки Q _3ф со сменным объемом трелевки в 50 м³. В связи с тем, что реально такой лесосеки нет – трелевка из нее не производится, полагаем, что себестоимость трелевки с этой лесосеки равняется нулю.

Аналогичный прием можно использовать, если объем поставок больше объема потребления – объем трелевки с лесосек больше вместимости погрузочных пунктов. В этом случае вводится фиктивный погрузочный пункт. При введении фиктивной лесосеки Л_3ф появляются три дополнительные переменные х ₃₁, х ₃₂, х ₃₃, и ограничения с учетом выражений (5.14)–(5.15) примут следующий вид:

x ₁₁+ x ₁₂+ x ₁₃= Q ₁;

x ₂₁+ x ₂₂+ x ₂₃= Q ₂;

x ₃₁+ x ₃₂+ x ₃₃= Q _3ф;

x ₁₁+ x ₂₁+ x ₃₁= V ₁;

x ₁₂+ x ₂₂+ x ₃₂= V ₂;

x ₁₃+ x ₂₃+ x ₃₃= V ₃;

Итак, окончательная постановка задачи выглядит следующим образом: минимизировать

у = 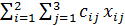=2 х ₁₁+1,5 x ₁₂+4 х ₁₃+З x ₂₁+2 х ₂₂+1 x ₂₃;

при ограничениях

x ₁₁+ x ₁₂+ x ₁₃= Q ₁;

x ₂₁+ x ₂₂+ x ₂₃= Q ₂;

x ₃₁+ x ₃₂+ x ₃₃= Q ₃;

x ₁₁+ x ₂₁+ x ₃₁= V ₁;

x ₁₂+ x ₂₂+ x ₃₂= V ₂;

x ₁₃+ x ₂₃+ x ₃₃= V ₃; (5.17)

x_ij 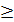0 для всех значений i и j. Аналогично ставятся другие транспортные задачи.

5.4.3.3. Алгебраическое решение задачи методом потенциалов.

Алгоритм решения транспортной задачи методом потенциалов включает в себя следующую последовательность шагов:

1) нахождение начального допустимого решения;

2) выделение из числа небазисных переменных переменной, включаемой в базис; если все небазисные переменные удовлетворяют условию оптимальности симплекс-метода (см. разд. 5.3.8.3), то закончить вычисления, иначе перейти к шагу 3;

3).нахождение исключаемой из базиса переменной, используя условие допустимости симплекс-метода (см. разд. 5.3.8.3) из числа переменных текущего базиса, нахождение нового базисного решения и переход к шагу 2.