Общие положения

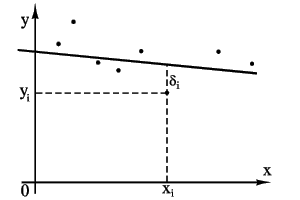
Для упрощения изложения рассмотрим сначала случай линейной функции одного аргумента. Пусть из опыта получены точки:

x₁, y₁,
x₂, y₂,...		(1)
x_n, y_n

(см. рисунок). Требуется найти уравнение прямой

y=ax+b,

(2)

наилучшим образом согласующейся с опытными точками.

Пусть мы нашли такую прямую. Обозначим через 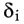расстояние опытной точки от этой прямой (измеренное параллельно оси y).

Из уравнения (2) следует, что

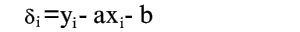
(3)

Чем меньше числа 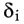по абсолютной величине, тем лучше подобрана прямая (2). В качестве характеристики точности подбора прямой (2) можно принять сумму квадратов

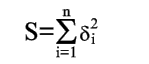
(4)

Покажем, как можно подобрать прямую (2) так, чтобы сумма квадратов S была минимальной. Из уравнений (3) и (4) получаем

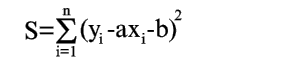
(5)

Условия минимума S будут

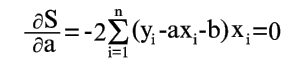
	(6)
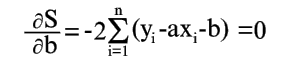
	(7)

Уравнения (6) и (7) можно записать в таком виде:

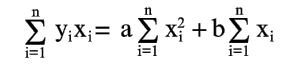
	(8)
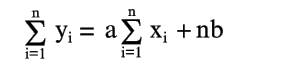
	(9)

Из уравнений (8) и (9) легко найти a и b по опытным значениям x_i и y_i. Прямая (2), определяемая уравнениями (8) и (9), называется прямой, полученной по методу наименьших квадратов (этим названием подчеркивается то, что сумма квадратов S имеет минимум). Уравнения (8) и (9), из которых определяется прямая (2), называются нормальными уравнениями.

Можно указать простой и общий способ составления нормальных уравнений. Используя опытные точки (1) и уравнение (2), можно записать систему уравнений для a и b

y₁=ax₁+b,
y₂=ax₂+b,...		(10)
y_n=ax_n+b,

Умножим левую и правую части каждого из этих уравнений на коэффициент при первой неизвестной a (т.е. на x₁, x₂,..., x_n) и сложим полученные уравнения, в результате получится первое нормальное уравнение (8).

Умножим левую и правую части каждого из этих уравнений на коэффициент при второй неизвестной b, т.е. на 1, и сложим полученные уравнения, в результате получится второе нормальное уравнение (9).

Этот способ получения нормальных уравнений является общим: он пригоден, например, и для функции

y=a₀+a₁x+a₂x²+...+a_nxⁿ.

(11)

Естественно, что здесь получится система из n+1 нормального уравнения для определения величин
a₀, a₁, a₂,..., a_n.

Рассмотрим частный случай применения метода наименьших квадратов. Пусть из теории известно, что

k=y/x

(12)

есть величина постоянная и ее нужно определить по опытным данным (1).

Систему уравнений для k можно записать:

k=y₁/x₁,
k=y₂/x₂,...		(13)
k=y_n/x_n,

Для получения нормального уравнения умножим каждое из этих уравнений на коэффициент при неизвестной k, т.е. на 1, и сложим полученные уравнения

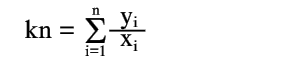
(14)

отсюда

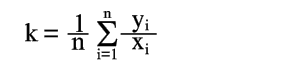
(15)

Следовательно, среднее арифметическое, полученное из опытных отношений y_i/x_i, дает решение поставленной задачи по методу наименьших квадратов. Это важное свойство средней арифметической объясняет ее широкое применение в практике обработки опытных данных.