- В треугольнике ABC известно:
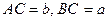/ Медианы 
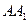и 
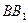перпендикулярны. Найдите площадь треугольника. - Докажите, что медианы треугольника ABC перпендикулярны в том и только том случае, когда
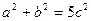. - Докажите, что для четырех произвольных точек A, B, C, D имеет место равенство
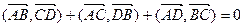. - CM – высота треугольника ABC, H – его ортоцентр. Докажите, что
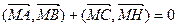. - Докажите, что высоты треугольника (или их продолжения) пересекаются в одной точке.
- Точка O – центр описанной окружности треугольника ABC, точка H такова, что
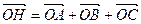. Докажите, что H – ортоцентр треугольника. - Для любого вектора
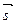имеет место равенство 
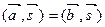. Докажите, что 
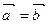. - Выведите формулу Герона вычисления площади треугольника.
- Внутри правильного n -угольника взята точка, проекции которой на все стороны попадают во внутренние точки сторон. Этими точками стороны разделяются на 2 n отрезков. Занумеруем их подряд: 1, 2, 3,..., 2 n. Доказать, что сумма длин отрезков с чётными номерами равна сумме длин отрезков с нечётными номерами.
- Правильный многоугольник
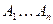вписан в окружность радиуса R с центром O, X — произвольная точка. Докажите, что 
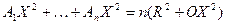. - О построении правильных многоугольников.
- В правильном пятиугольнике ABCDE диагонали AC и BD пересекаются в точке M. Докажите, что
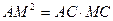и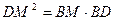 
. - У правильного 5000-угольника покрашено 2001 вершина. Докажите, что найдутся три покрашенные вершины, лежащие в вершинах равнобедренного треугольника.
- В правильном 10-угольнике провели все диагонали. Сколько попарно неподобных треугольников имеется на этом рисунке?
Скалярное произведение. Правильные многоугольники
2015-08-21
585Поделись с друзьями:
|
|
Сейчас читают про:
8213
8054