Даны координаты вершин треугольника А, В, С. Найти:
- уравнения прямы, содержащих стороны треугольника,
- длину высоты АD опущенной из вершины А на сторону ВС,
- уравнение медианы АЕ,
- уравнение прямой проходящей через точку А перпендикулярно прямой ВС.
| № | А | В | С | |
| {4;-2} | {3;2 } | {-1;-10} | ||
Решение.
1. уравнения прямы, содержащих стороны треугольника
Сторона АВ:
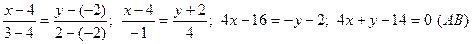
Сторона АС:
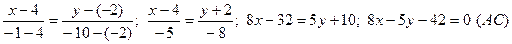
Сторона ВС:
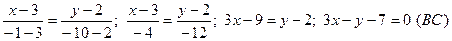
2. длину высоты АD опущенной из вершины А на сторону ВС
Длина высоты АD – это расстояние от точки до прямой ВС, которое можно найти по формуле:
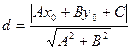 , где
, где 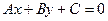 - уравнение прямой, (х0, у0) – координаты точки.
- уравнение прямой, (х0, у0) – координаты точки.
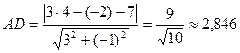
3. уравнение медианы АЕ
AЕ – медиана, значит точка Е – середина ВС, найдем ее координаты по формуле середины отрезка:
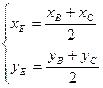 =>
=> 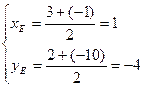
Е(1; -4)
Тогда уравнение AЕ:
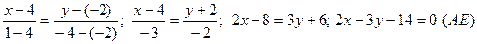
4. уравнение прямой, проходящей через точку А, перпендикулярно прямой ВС.
Прямая s 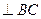 , значит по условию перпендикулярности ее угловой коэффициент равен:
, значит по условию перпендикулярности ее угловой коэффициент равен: 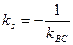 .
.
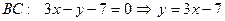 ,
, 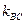 =3.
=3.
Тогда уравнение высота s:
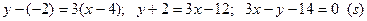
 2015-08-12
2015-08-12 973
973








