2015-08-12
462
Челябинский государственный университет
Контрольная работа №1
По высшей математике
| № зачетной книжки: | |
| № варианта: | |
| Форма обучения: | заочная |
| Специальность: | |
| Курс: | |
| Группа: | |
| Выполнил: |
| Номера задач по варианту: | |||||
| Зачтено: |
Челябинск 2012
Задачи контрольной работы №1
Задачи № 1- 30.
Выполнить действия над матрицами.
15. 
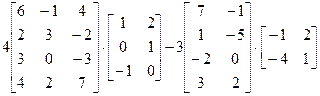
Решение.
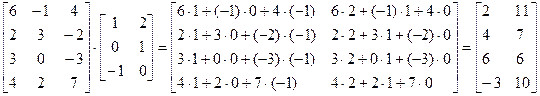
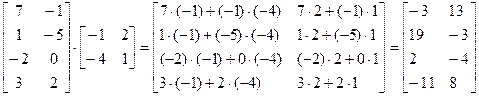
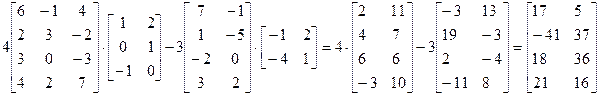
Задачи № 31- 60.
Решить систему:
· по формулам Крамера, (см. список литературы № 1, стр.33)
Сделать проверку.
46. 
|
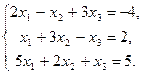
Решение.
Вычислим главный определитель системы:
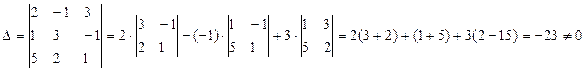- значит, система имеет единственное решение.
Вспомогательные определители:
= 
; 
= 
; 
= 
.
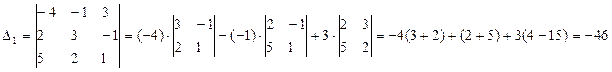
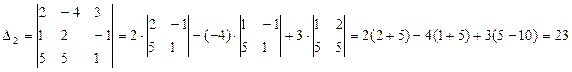
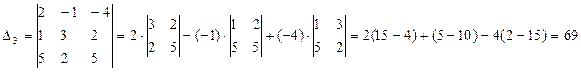
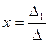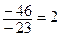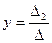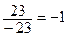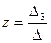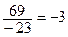Проверка:
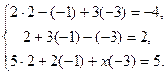
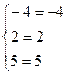
Ответ.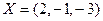 
Задачи № 61- 90.
Исследовать систему уравнений и решить ее, если она совместна, методом Гаусса. Найти:
· ее общее решение,
· частное решение.
Cделать проверку.
77. 
|
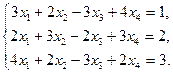
Решение.
Дана неоднородная линейная система из трех уравнений с четырьмя неизвестными (m = 3, n = 4). Выпишем матрицы системы линейных уравнений:
, 
, 
.
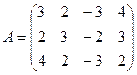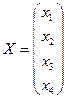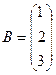1) определим, совместна или нет система.
Вычислим для этого ранги расширенной и основной матриц системы: Rang(A,B) и Rang(A). Для этого приведем матрицу (А,В) к матрице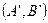 
, имеющую ступенчатую форму.
(А,В)=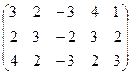 
~ 
~ 
~
~ 
~ 
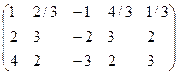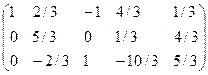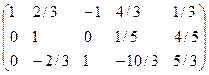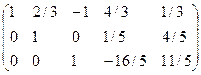
Привели матрицу (А,В) к матрице 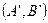, имеющую ступенчатую форму.
= .
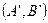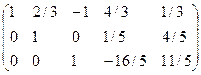Rang 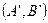= Rang(A,B) = Rang(A) = 3. Следовательно, система совместна.
2) так как Rang(A) < n (n = 4), то система имеет бесконечное множество решений. Найдем все решения системы. Для этого перейдем к следующей эквивалентной системе, используя коэффициенты уравнений расширенной матрицы ступенчатого вида .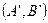
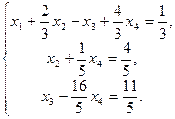
Пусть х1, х2, х3 – основные (базисные) неизвестные: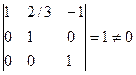 
.
Тогда х4 – свободная (небазисная) переменная, и можно считать х4= а, где а – произвольное число.
Решая эту систему из четырех уравнений с пятью неизвестными х1, х2, х3, х4 найдем их:
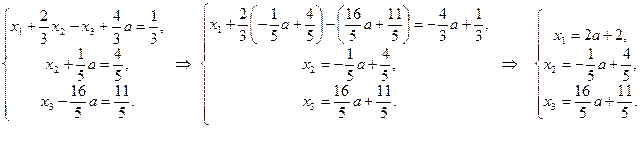
Общее уравнение системы: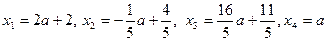 
.
3) Найдем базисное решение СЛУ из общего решения системы, для этого приравняем все свободные переменные нулю.
Пусть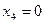 
, тогда 
.
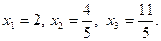Базисное решение имеет вид: (2,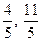 
, 0).
4) найдем частное решение системы из общего решения:
Например, а = 1, тогда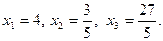 
Проверка:
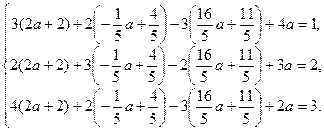
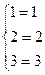
Верно.
