В лабораторной работе вращающаяся система представляет собой вал со шкивом и крестовиной так называемый крестообразный маятник Обербека (рисунок). На стержни крестовины можно симметрично насаживать два (или четыре) тела массой 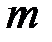 на расстояниях
на расстояниях 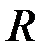 от оси вращения и прочно закреплять их винтами. На шкив радиусом
от оси вращения и прочно закреплять их винтами. На шкив радиусом 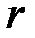 наматывается нить, к концу которой привязывается груз массой
наматывается нить, к концу которой привязывается груз массой 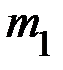 . В исходном состоянии система заторможена. После снятия с тормоза, груз
. В исходном состоянии система заторможена. После снятия с тормоза, груз 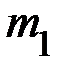 ускоренно движется вниз, а вал с крестовиной и телами
ускоренно движется вниз, а вал с крестовиной и телами 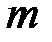 ускоренно вращаются.
ускоренно вращаются.
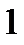
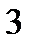
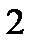
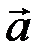
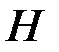
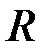
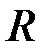
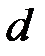
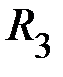
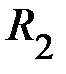
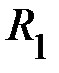
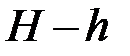
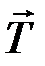
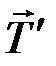
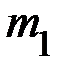
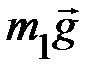
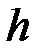
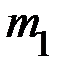
Рис. 1. Схема установки маятника Обербека:
1-исходное положение груза 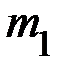 , 2-его конечное положение., 3-площадка
, 2-его конечное положение., 3-площадка
Обозначим 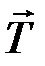 – силу натяжения нити, приложенную по касательной к шкиву вала. Такая же по величине, противоположная по направлению, реакция нити
– силу натяжения нити, приложенную по касательной к шкиву вала. Такая же по величине, противоположная по направлению, реакция нити 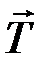 приложена к грузу
приложена к грузу 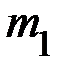 . Радиус шкива
. Радиус шкива 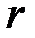 , ускорение
, ускорение 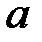 поступательного движения груза
поступательного движения груза 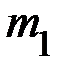 и угловое ускорение
и угловое ускорение 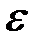 вала связаны очевидным соотношением
вала связаны очевидным соотношением 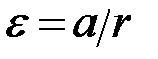 . Применим к грузу
. Применим к грузу 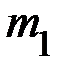 второй закон динамики для поступательного движения (в проекции на направление движения)
второй закон динамики для поступательного движения (в проекции на направление движения) 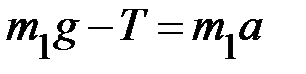 . Откуда натяжение нити
. Откуда натяжение нити 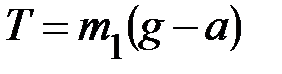 . К вращающемуся телу (системе тел) применим второй закон динамики для вращательного движения
. К вращающемуся телу (системе тел) применим второй закон динамики для вращательного движения 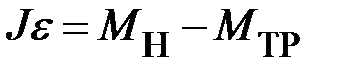 , где
, где  – момент инерции всего вращающегося тела (или системы вращающихся тел). Момент силы натяжения нити
– момент инерции всего вращающегося тела (или системы вращающихся тел). Момент силы натяжения нити 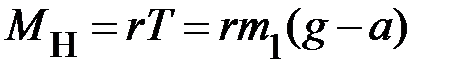 . Момент силы трения в подшипниках, препятствующий вращению
. Момент силы трения в подшипниках, препятствующий вращению 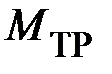 . Из II закона Ньютона момент инерции вращающегося тела
. Из II закона Ньютона момент инерции вращающегося тела 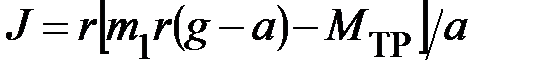 .
.
При постоянной массе всей системы момент силы трения можно считать величиной постоянной. Значит и ускорение 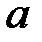 тоже постоянно, то есть поступательное движение груза
тоже постоянно, то есть поступательное движение груза 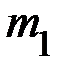 и вращательное движение вала является равноускоренным. Груз
и вращательное движение вала является равноускоренным. Груз 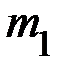 движется параллельно вертикальной стойке с делениями (линейке). В исходном положении донышко груза устанавливается против верхнего конца линейки. В нижней части линейки имеется площадка 3 (см. рисунок), о которую груз ударяется. Из формулы пути равноускоренного движения
движется параллельно вертикальной стойке с делениями (линейке). В исходном положении донышко груза устанавливается против верхнего конца линейки. В нижней части линейки имеется площадка 3 (см. рисунок), о которую груз ударяется. Из формулы пути равноускоренного движения 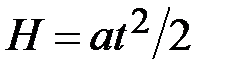 находим ускорение
находим ускорение 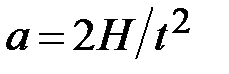 груза
груза 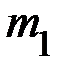 , где
, где 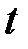 – время с момента пуска до момента удара груза
– время с момента пуска до момента удара груза 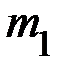 о площадку
о площадку 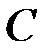 ;
; 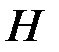 − высота падения Для внешних точек шкива тангенциальное ускорение
− высота падения Для внешних точек шкива тангенциальное ускорение 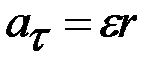 , а ускорение, направленное по нормали,
, а ускорение, направленное по нормали, 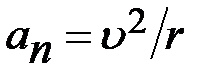 . Для тела
. Для тела 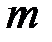 , вращающегося по окружности на расстоянии
, вращающегося по окружности на расстоянии 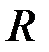 , тангенциальное ускорение
, тангенциальное ускорение 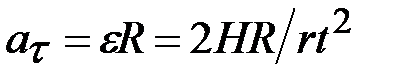 и ускорение, направленное по нормали,
и ускорение, направленное по нормали, 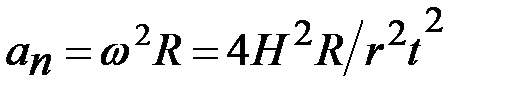 .
.
Момент силы трения 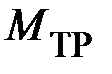 можно определить различными способами. Один из них заключается в следующем. Длину нити подбирают так, чтобы сразу после удара груза
можно определить различными способами. Один из них заключается в следующем. Длину нити подбирают так, чтобы сразу после удара груза 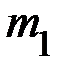 о площадку
о площадку 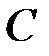 при дальнейшем вращении крестовины по инерции нить стала наматываться, а груз
при дальнейшем вращении крестовины по инерции нить стала наматываться, а груз 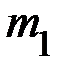 равнозамедленно подниматься до полной остановки. В момент остановки фиксируют крестовину тормозом и измеряют по линейке расстояние
равнозамедленно подниматься до полной остановки. В момент остановки фиксируют крестовину тормозом и измеряют по линейке расстояние 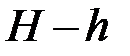 , на которое груз не дошёл до исходного состояния (рисунок). Потенциальная энергия груза в конечном состоянии оказывается меньше, чем в начальном на величину
, на которое груз не дошёл до исходного состояния (рисунок). Потенциальная энергия груза в конечном состоянии оказывается меньше, чем в начальном на величину 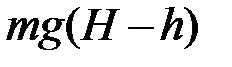 . Эта энергия израсходована на совершение работы по преодолению сил трения
. Эта энергия израсходована на совершение работы по преодолению сил трения 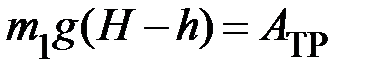 . С учётом примерного равенства момента силы трения при спуске и подъеме по формуле работы при вращательном движении запишем
. С учётом примерного равенства момента силы трения при спуске и подъеме по формуле работы при вращательном движении запишем 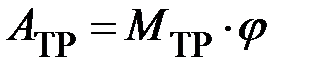 , где
, где 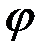 – угол поворота от начального до конечного состояния. По определению радианной меры угла
– угол поворота от начального до конечного состояния. По определению радианной меры угла 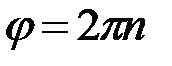 , где число оборотов
, где число оборотов 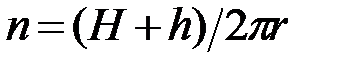 , запишем
, запишем 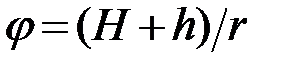 . Момент силы трения
. Момент силы трения 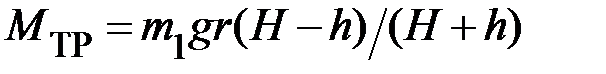 . Переходя от радиуса шкива к диаметру
. Переходя от радиуса шкива к диаметру 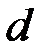 , т.к. его удобнее измерять штангенциркулем, для опытного определения момента инерции твёрдого тела вокруг неподвижной оси с учётом сил трения получим окончательную формулу
, т.к. его удобнее измерять штангенциркулем, для опытного определения момента инерции твёрдого тела вокруг неподвижной оси с учётом сил трения получим окончательную формулу
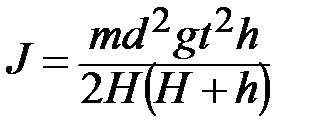 . (1)
. (1)
Запишем упрощённую формулу расчёта момента инерции твёрдого тела вокруг неподвижной оси без учёта сил трения
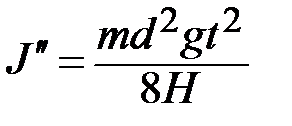 . (2)
. (2)
Расчёт погрешности. Выразим допускаемую из опыта относительную ошибку 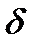 при определении момента инерции без учёта сил трения
при определении момента инерции без учёта сил трения
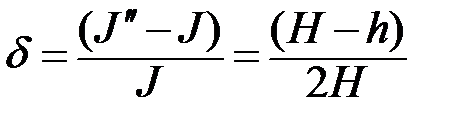 . (3)
. (3)
Из формулы (1) находим расчётную относительную погрешность в определении момента инерции
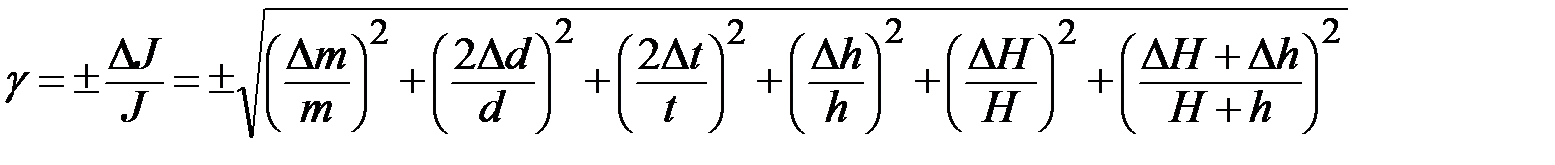 . (4)
. (4)
и его абсолютную погрешность
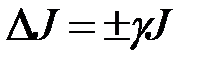 .
.
 2015-08-12
2015-08-12 541
541








