Для анализа формы траектории оба уравнения должны быть выражены относительно одной гармонической функции (sin и sin или cos и cos). Отметим, что 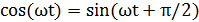 и
и 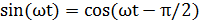
Если частоты одинаковы и разность фаз 0, 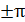 , … – прямая линия.
, … – прямая линия.
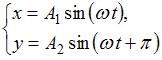 – 1.
– 1.
Если частоты одинаковы и разность фаз 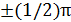 ,
, 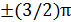 ,… – эллипс.
,… – эллипс.
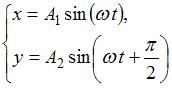 – нет графика.
– нет графика.
и одинаковые амплитуды – окружность.
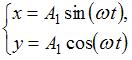 – 2.
– 2.
Если частоты кратны друг другу – фигуры Лиссажу.
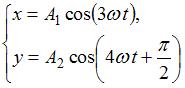 – 3.
– 3.
8. Складываются взаимно перпендикулярные колебания. Установите соответствие между законами колебания точки 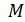 вдоль осей координат
вдоль осей координат 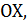
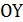 и формой траектории.
и формой траектории.
1. 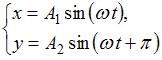 2.
2. 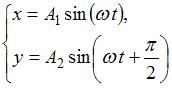 3.
3. 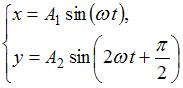
| прямая линия | ||
| эллипс | ||
| фигура Лиссажу | ||
| cинусоида |
 2015-08-12
2015-08-12 954
954








