Рисунок смотри выше. В МКТ в качестве неизвестных выступают контурные токи, это абстракные величины; контурные токи замыкаются по независимым контурам. Причем если в схеме есть источник тока, то через каждый источник замыкается по 1-му контурному току, величина которых в дальнейшем считается известной и равной токам источников. I33=J6. Выразим токи в ветвях через контурные токи, для этого I1=I11, I2=I22-I11, I3=I22, I4=I11-I33, I5=I22-I33}. Подставим это в уравнение состояний по 2-му закону Кирхгофа и сгруппируем слагаемые {(R1+R2+R4)I11-R2I22-
-R4I33=E1-E2-E4, -R2I11+(R2+R3’+R3’’+R5)I22-R5I33=E2-E5, I33=J6}. Полученная система называется системой контурных уравнение. Можно представить в формализованном виде. {R11I11+R12I22+R13I33=E11,
R21I11+R22I22+R23I33=E22, I33=J6}; Rkk – контурное сопротивление, оно равно сумме всех сопротивлений входящих в данный контур, R11=R4+R1+R2, R22=R5+R3’+R3’’; Rkj – сопротивление ветвей общих для k-го и j-го контуров. Rkj со знаком +, если направление k-го и j-го контурных токов через эту ветвь совпадают, и -, если нет; Rkj=Rjk;
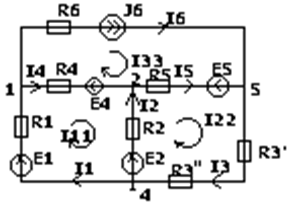 R12=R21= -R2, R13= -R4, R23= - R5; Ekk – контурное ЭДС равное сумме ЭДС контура; E11=E1-E2-E4; E22=E2-E5. Найденные контурные токи подставляются в первоначальную систему и находятся все токи.
R12=R21= -R2, R13= -R4, R23= - R5; Ekk – контурное ЭДС равное сумме ЭДС контура; E11=E1-E2-E4; E22=E2-E5. Найденные контурные токи подставляются в первоначальную систему и находятся все токи.
19. Метод узлового напряжения. Цепь, имеющая два узла, к которым подключены n параллельных ветвей. Необходимо: 1) указать условно положительное направление токов; 2) указать условно положительное направление напряжений между узлами; 3) по формуле определяют напряжение между двумя узлами; 4) обобщенный закон Ома => определить токи во всех ветвях; 5) проверка – баланс мощностей.
20. Метод эквивалентного генератора.
Метод эквивалентного генератора
Метод применяется, если полный расчёт схемы не нужен, а необходимо определить токи только в одной или нескольких ветвях.
Этот метод также называют теоремой об активном двухполюснике. Читается теорема следующим образом:
Любую электрическую цепь по отношению к исследуемой ветви можно представить в виде эквивалентного генератора, содержащего эквивалентный источник ЭДС ЕЭ и эквивалентное внутреннее сопротивление ZВН; (Рис. 55).

Напряжение на выходе эквивалентного генератора находится из выражения:
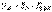 .
.
Определить параметры эквивалентного генератора можно из опытов холостого хода (хх) и короткого замыкания (кз).
В эти опыты моделируются математически или физически.
Опыт холостого хода. (Рис. 56).

Подставим в выражение 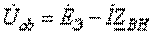 значение тока
значение тока  , получим
, получим 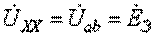 .
.
Второй опыт – короткого замыкания. (Рис. 57).

Из закона Ома получим:
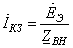 , откуда выразим
, откуда выразим 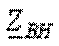 как
как 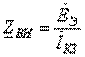 .
.
Зная параметры эквивалентного генератора определим ток, протекающий по нагрузке:
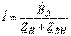 .
.
21. Метод наложения используется для расчёта эл. цепи принципом суперпозиций. По этому методу в ветвях, содержащих ЭДС, исключая ЭДС, все кроме первого. Определяют известными методами токи во всех ветвях. Действующие токи определяют как алгебраическую сумму токов от каждой ЭДС в отдельности.
Метод наложения.
Метод формулируется так:
Ток в любой ветви электрической схемы равен алгебраической сумме токов, наводимых в этой ветви каждым из источников в отдельности.
Пояснить этот метод проще и наглядней рисунком

Пусть требуется рассчитать схему, показанную на рисунке а.
Исходя из определения метода, можно записать для тока в любой ветви:
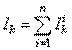 , где n – число ветвей схемы, содержащих источники энергии.
, где n – число ветвей схемы, содержащих источники энергии.
Для того, чтобы определить токи 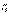 исключим поочередно из схемы сначала источник ЭДС Е1 (см. рисунок б), а затем источник ЭДС Е2 (см. рисунок в), оставив при этом внутренние сопротивления источников в схеме. В нашем случае будем считать источники ЭДС идеальными, т.е. с нулевыми внутренними сопротивлениями.
исключим поочередно из схемы сначала источник ЭДС Е1 (см. рисунок б), а затем источник ЭДС Е2 (см. рисунок в), оставив при этом внутренние сопротивления источников в схеме. В нашем случае будем считать источники ЭДС идеальными, т.е. с нулевыми внутренними сопротивлениями.
Токи в схеме б определим по формулам:
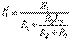 ,
, 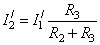 и
и 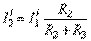 .
.
Токи в схеме в определим по формулам:
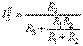 ,
, 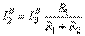 и
и 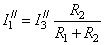 .
.
Зная токи, наводимые в ветвях каждым из источников в отдельности, найдем токи в исходной схеме:
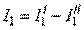 ;
;
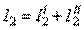 ;
;
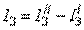 .
.
22. Применение переменного тока и основные определения величин параметров: периода, частоты, угловой частоты, мгновенных и амплитудных значений тока, напряжения и ЭДС. Периодические величины изменяются по времени и по направлению, повторяются через одинаковые промежутки времени (периоды (T)). Частота f=1/Т (Гц=с-1). Угловая частота ω=2πf (рад/с). i = Imsin(ωt + ψi), где ψi – начальная фаза, Im – максимальное значение (амплитуда) тока, i – мгновенное значение синусоидального тока. Период – наименьший промежуток времени, по истечению которого мгновенные значения тока повторяются. Частота периодического тока – число периодов в секунду.Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими,а наименьший промежуток времени, через который эти повторения наблюдаются, - периодом Т. Для периодического тока имеем 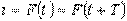 , ,
| |
Величина, обратная периоду, есть частота, измеряемая в герцах (Гц): 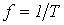 , ,
|
Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц. Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой: i - мгновенное значение тока 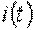 ; u – мгновенное значение напряжения
; u – мгновенное значение напряжения 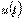 ; е - мгновенное значение ЭДС
; е - мгновенное значение ЭДС 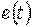 ; р - мгновенное значение мощности
; р - мгновенное значение мощности 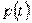 .Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m).
.Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m).
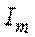 - амплитуда тока;
- амплитуда тока;
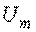 - амплитуда напряжения;
- амплитуда напряжения;
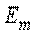 - амплитуда ЭДС.
- амплитуда ЭДС.
23. Получение синусоидальных ЭДС. Согласно закону электромагнитной индукции при изменении потокосцепления витка в нём индуцируется ЭДС, положительное направление которой связывают с положительным направлением потока Фх правилом буравчика (правого винта).
Пусть в однородном магнитном поле NS (рис.4.4) равномерно вращается рамка, активные стороны которой a и b, расположенные перпендикулярно к плоскости чертежа и пересекающие линии магнитной индукции, движутся с некоторой линейной скоростью  . При этом в них будут наводится ЭДС по закону Фарадея и по правилу правой руки.
. При этом в них будут наводится ЭДС по закону Фарадея и по правилу правой руки.
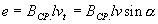 где
где 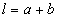 ,
, 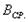 -среднее значение индукции.
-среднее значение индукции.
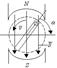 Рис. 4.4 Рис. 4.4 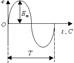
|
Для данной рамки 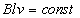 и при
и при 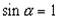
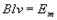 - амплитуда ЭДС.
- амплитуда ЭДС.
Так как 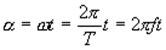 ;
; 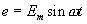
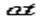 -фаза колебания,
-фаза колебания,
Т-период, 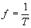 -частота. (От частоты зависят потери в сердечниках и проводах).
-частота. (От частоты зависят потери в сердечниках и проводах).
Наиболее оптимальная частота 50-60 Гц.
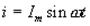 можно получить, используя закон Ома
можно получить, используя закон Ома 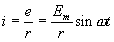 .
.
Синусоидальную ЭДС можно получить и другим способом.
На современных электростанциях электрическая энергия получается от генераторов переменного тока, приводимых в движение механическими двигателями (преимущественно паровыми и гидравлическими турбинами). Работа электромагнитных генераторов основана на законах электромагнитной индукции и электромагнитных сил.
Генератор переменного тока (рис.4.5) состоит из двух основных частей — вращающегося ротора и неподвижного статора. На роторе расположены полюсы, т.е. электромагниты, обмотка которых питается от источника постоянного тока относительно небольшой мощности. Полюса создают магнитный поток машины. На цилиндрическом статоре расположена в пазах основная обмотка генератора, в которой индуцируется переменная ЭДС.
На рис.4.5 показана схема устройства двухполюсного генератора синусоидального тока
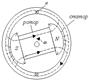 Рис. 4.5 Рис. 4.5
|
На рис.4.5 для простоты обмотка ротора опущена и изображены только полюсы N и S, а на статоре показаны два проводника а и b одного витка обмотки.
Сердечники статора и ротора изготовляют из стали. Магнитный поток Ф машины проходит через ферромагнитный материал на всем своем пути, за исключением двух небольших воздушных промежутков (зазоры), отделяющих ротор от статора.
При вращении ротора с постоянной угловой скоростью 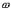 в каждом проводнике статорной обмотки наводится по закону Фарадея ЭДС
в каждом проводнике статорной обмотки наводится по закону Фарадея ЭДС 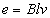 ,
,
где активная длина проводника 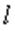 и линейная скорость перемещения магнитного поля
и линейная скорость перемещения магнитного поля 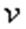 остаются в процессе работы генератора неизменными. Характер изменения ЭДС
остаются в процессе работы генератора неизменными. Характер изменения ЭДС 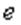 определяется законом распределения магнитной индукции
определяется законом распределения магнитной индукции 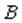 в воздушном зазоре машины.
в воздушном зазоре машины.
Для получения синусоидальной ЭДС полюсному наконечнику, обращенному к статору, придают такое очертание, при котором воздушный зазор увеличивается от середины полюса к его краям. Благодаря неравенству магнитных сопротивлений в различных частях воздушного зазора магнитная индукция имеет максимальные значения у середины полюса, где воздушный зазор минимален. По мере приближения к краям каждого полюса магнитная индукция постепенно убывает по закону синуса (рис.4.6).
Момент, когда вращающийся ротор займет горизонтальное положение, примем за начало отсчета времени t=0 (рис.4.7, а).
В месте расположения проводников а и b магнитная индукция В=0, поэтому индуцируемая в этих проводниках ЭДС 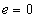 .
.
В произвольный момент времени t, когда ротор повернется на угол 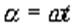 (рис.4.7,б), магнитная индукция в месте расположения проводников а и b будет равна
(рис.4.7,б), магнитная индукция в месте расположения проводников а и b будет равна 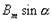 . В этих проводниках индуцируются одинаковые по величине ЭДС
. В этих проводниках индуцируются одинаковые по величине ЭДС 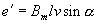 .
.
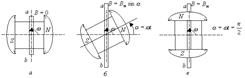
Рис. 4.7
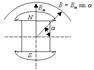 Рис. 4.6 Рис. 4.6
|
Применяя правило правой руки к каждому из двух стержней витка аb, можно убедиться, что электродвижущие силы, индуктируемые в этих стержнях, действуют в витке в одном и том же направлении. Потому общий ЭДС в витке будет равна
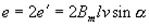 (1) Наибольшее значение ЭДС будет в витке при
(1) Наибольшее значение ЭДС будет в витке при 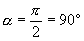 (рис. 4.7,в)
(рис. 4.7,в)
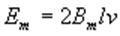 (2) Исходя из формул (1) и (2) и учитывая, что
(2) Исходя из формул (1) и (2) и учитывая, что 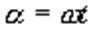 получаем
получаем
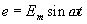 (3)
(3)
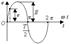 Рис. 4.8 Рис. 4.8
|
На рис.4.8 показан график изменения синусоидальной ЭДС за один полный оборот ротора.
ЭДС, наводимая в одном витке, относительно невелика. Для получения значительных ЭДС статорную обмотку выполняют из большого числа последовательно соединенных витков.
24. Действующие и средние значения синусоидальных величин. Для количественной оценки синусоидального тока используется значение постоянного тока, эквивалентное синусоидальному по совершаемой работе. Действующим значением синус. тока назыв. такое значение постоянного тока, при прохождении которого в одном и том же резисторе за время одного периода выделяется столько же теплоты, сколько при прохождении синус. тока: 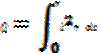 , i =
, i = 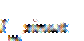 - переменный ток; Q = I2rT – постоянный ток.
- переменный ток; Q = I2rT – постоянный ток. 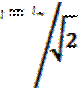 - действующее значение тока,
- действующее значение тока, 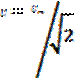 - действующее значение напряжения,
- действующее значение напряжения, 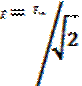 - действующее значение ЭДС. Среднее значение – среднее арифметическое:, i = Imsin ωt, Iср = 2Im/π, Uср = 2Um/ π, Eср = 2Em/ π.
- действующее значение ЭДС. Среднее значение – среднее арифметическое:, i = Imsin ωt, Iср = 2Im/π, Uср = 2Um/ π, Eср = 2Em/ π.
 2015-08-13
2015-08-13 550
550






