Пару полярных координат 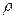 и
и 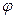 можно перевести в Декартовы координаты x и y путём применения тригонометрических функций синуса и косинуса:
можно перевести в Декартовы координаты x и y путём применения тригонометрических функций синуса и косинуса:
x = 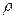 cos
cos 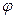 ,
,
y = 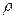 sin
sin 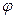 ,
,
в то время как две декартовы координаты x и y могут быть переведены в полярную координату 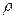 :
:
r2 = y2 + x2 (по теореме Пифагора).
3.Определение геометрического вектора, вычисление его длины (модуля) для случаев задания: начальной 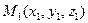 и конечной
и конечной 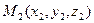 точками; и в виде
точками; и в виде 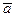 =
= 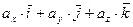 =
= 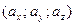 .
.
а ) Геометрическим вектором а называется множество всех направленных векторов, имеющих одинаковую длину и направление. О всяком отрезке 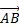 из этого множества говорят, что он представляет вектор a (получен приложением вектора a к точке А). Длинна отрезка
из этого множества говорят, что он представляет вектор a (получен приложением вектора a к точке А). Длинна отрезка 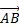 называется длинной (модулем) вектора а и обозначается символом
называется длинной (модулем) вектора а и обозначается символом 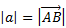 . Вектор нулевой длины называется нулевым вектором и обозначается символом 0.
. Вектор нулевой длины называется нулевым вектором и обозначается символом 0.
б) Зная координаты начала и конца вектора, мы можем вычислить координаты вектора по формуле:
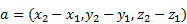
Зная координаты вектора модуль вектора вычисляется по формуле:
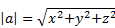
4. Геометрический смысл и физический смысл линейных операций с векторами: сумма векторов 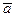 ,
, 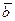 и умножение вектора
и умножение вектора 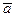 на вещественное число
на вещественное число 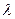 .
.
а) Суммой двух векторов 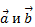 называется вектор, имеющий начало в начале вектора
называется вектор, имеющий начало в начале вектора 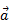 , а конец – в конце вектора
, а конец – в конце вектора 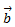 , при условии, что вектор
, при условии, что вектор 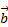 приложен к концу вектора
приложен к концу вектора 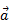 .
.
В соответствии с определением слагаемые 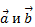 и их сумма
и их сумма 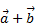 образуют треугольник (рис.ниже). Поэтому данное правило сложения двух векторов называют «правилом треугольника».
образуют треугольник (рис.ниже). Поэтому данное правило сложения двух векторов называют «правилом треугольника».
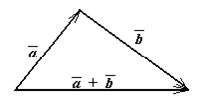 Операция сложения векторов обладает свойствами:
Операция сложения векторов обладает свойствами:
1. 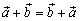 (коммутативность);
(коммутативность);
2. 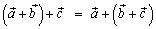 , (ассоциативность);
, (ассоциативность);
3. 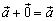 для любого вектора
для любого вектора 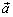 (особая роль нулевого вектора);
(особая роль нулевого вектора);
4. Для каждого вектора 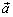 существует противоположный ему вектор
существует противоположный ему вектор 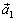 такой, что
такой, что 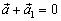 (для получения достаточно поменять местами начало и конец вектора).
(для получения достаточно поменять местами начало и конец вектора).
Вектор противоположный вектору 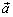 обозначают
обозначают 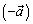
б) Произведением 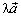 вектора
вектора 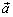 на вещественное число λ (скаляр) называется вектор
на вещественное число λ (скаляр) называется вектор 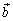 , такой, что 1)
, такой, что 1) 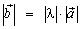 ; 2) вектор
; 2) вектор 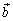 коллинеарен вектору
коллинеарен вектору 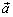 ; 3) векторы
; 3) векторы 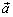 и
и 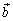 имеют одинаковое (противоположное) направление если λ > 0 (λ < 0).
имеют одинаковое (противоположное) направление если λ > 0 (λ < 0).
Замечание: В случае, когда λ = 0 или произведение является нулевым вектором.
7.Определение линейной зависимости совокупности векторов 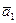 ,
, 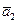 ,…,
,…, 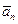 : привести два определения и показать их равносильность.
: привести два определения и показать их равносильность.
Пусть задана система векторов а1, а2, а3,…,аn (1) одной размерности.
Определение: система векторов (1) называется линейно-независимой, если равенство a1 а1+a2 а2+…+ an аn =0 (2) выполняется лишь в том случае, когда все числа a1, a2,…, an=0 и Î R
Определение: система векторов (1) называется линейно-зависимой, если равенство (2) выполнимо хотя бы при одном a i ¹ 0 (i=1,…,k)
Свойства
Если система векторов содержит нулевой вектор, то она линейно зависима
Если система векторов содержит линейно-зависимую подсистему векторов, то она будет линейно-зависимой.
Если система векторов линейно-независима, то и любая ее подсистема будет линейно независимой.
Если система векторов содержит хотя бы один вектор, являющийся линейной комбинацией других векторов, то эта система векторов будет линейно зависимой.
 2015-08-13
2015-08-13 2921
2921








