Определение определителя 3-го порядка как обобщение записи определителя 2-го порядка и геометрической схемы (правила) формирования членов определителя, то есть его вычисления

Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:

.

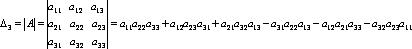Данная формула получила название правила треугольников или правило Сарруса.

При вычислении определителя 3-го порядка удобно пользоваться следующей схемой, показывающей произведения каких элементов берутся со знаком “+”, а каких со знаком “-“:

4.. Свойства определителя 3-го порядка, вытекающие из принятого правила его вычисления. Вычисление определителя 3-го порядка разложением по столбцу (строке).

а)Свойство 1. Если все элементы какой-либо строки (столбца) определителя 3-го порядка равны нулю, то и определитель равен нулю.

Свойство 2. Определитель 3-го порядка не изменится, если его строки заменить столбцами с теми же номерами.

Свойство 3. Если поменять местами две строки (столбца) определителя 3-го порядка, то обсолютная величина определителя не изменится, а знак изменится на противоположный.

Следствие. Определитель 3-го порядка, в котором каких-либо две строки (столбца) совпадают, равен нулю.

Свойство 4. Если все элементы какой-либо строки (столбца) определителя 3-го порядка умножить на какое-либо число, то и определитель умножится на это число.

Следствие 1. Если все элементы какой-либо строки (столбца) имеют общий множитель, то этот множитель можно вынести за знак определителя.

Следствие 2. Если все элементы какой-либо строки (столбца) определителя 3-го порядка пропорциональны соответствующим элементам другой строки (столбца) этого определителя, то определитель равен нулю.

Свойство 5. Если каждый элемент какой-либо строки (столбца) определителя 3-го порядка представляет собой сумму двух слагаемых, то и определитель можно представить в виде суммы двух слагаемых, например:

a₁b₁c₁ + d₁ a₁b₁c₁ a₃b₃c₃

a₂b₂c₂ + d₂ = a₂b₂с₂ + a₂b₂d₂

a₃b₃c₃ + d₃ a₃b₃c₃ a₃b₃d₃

б)Если D = |A| - определитель порядка n, то минором M_ij элемента а_ij называют определитель порядка n-1, получающийся из D вычеркиванием i-й строки и j-го столбца. Под алгебраическим дополнением A_ij элемента а_ij понимают минор M_ij, домноженный на (-1)^i+j, т.е. A_ij = (-1)^i+jM_ij

5.

Система трех линейных уравнений с тремя неизвестными имеет вид

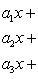
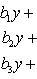
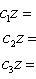
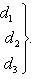(7)

Определитель

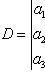
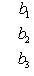
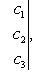(8)

составленный из коэффициентов при неизвестных, называется определителем системы.

1. Если определитель системы, то система (7) имеет решение, и притом единственное. Это решение находится по формулам

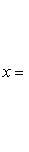
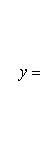
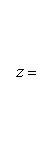
(9)

Из этого заключаем, что значение неизвестного системы (7) равно дроби, знаменатель которой есть определитель системы, а числитель есть определитель, получающийся из определителя системы заменой в нем столбца из коэффициентов при определяемом неизвестном столбцом свободных членов.

Определители, стоящие в числителях дробей (9), будем обозначать соответственно через D_x, D_y, D_z.

2. Если D = 0, но, по крайней мере, один из его миноров и хотя бы один из определителей D_x, D_y и D_z не равен нулю, то система (7) решений не имеет. В этом случае говорят, что она противоречива, или несовместна.

3. Если D = 0 и все определители, стоящие в числителях дробей (9), - D_x, D_y, D_z - равны нулю, т. е. если

D = D_x = D_y = D_z = 0,

но хотя бы один из миноров в определителе D не равен нулю, то одно уравнение системы (7) является следствием двух других, и система трех уравнений (9) приводится к двум уравнениям, причем решения этих двух уравнений удовлетворяют третьему. В этом случае система (9) имеет бесконечное множество решений и называется неопределенной.

4. Если же все миноры в определителе D равны нулю, но хотя бы один из миноров в каком-нибудь из определителей Dx, Dy, Dz не равен нулю и хотя бы один из коэффициентов при неизвестных не равен нулю, то система несовместна и решений не имеет.

5. Если в определителях D, Dx, Dy, Dz все миноры равны нулю, но хотя бы один из коэффициентов при неизвестных нулю не равен, то два уравнения системы являются следствием третьего, и система трех уравнений приводится к одному уравнению, является неопределенной и имеет бесконечное множество решений, причем решения этого третьего уравнения удовлетворяют первому и второму уравнениям.