2015-08-13
2410
НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ
Функцію F(x) називають первісною для функції f(x) на проміжку Х, якщо в кожній точці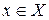 
виконується умова 
.
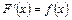Множину всіх первісних для функції f(x) на проміжку Х називають невизначеним інтегралом від функції f(x) і позначають так:
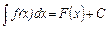, (6.1)
де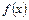 
– підінтегральна функція; 
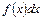– підінтегральний вираз; 
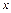– змінна інтегрування; 
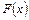– одна з первісних; 
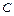– довільне дійсне число; 
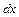– диференціал аргументу функції. Він визначає змінну по якій ведеться інтегрування.
Наприклад:
, 
, 
.
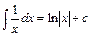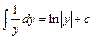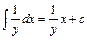Тому наявність диференціала під інтегралом є необхідним. Такий вираз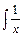 
немає змісту. Не відомо по якій змінній ведеться інтегрування.
Операцію знаходження невизначеного інтеграла по іншому називають інтегруванням функції.
Таким чином, операція інтегрування функції є оберненою до операції диференціювання. Щоб перевірити чи вірно проінтегрована функція слід продифереціювати результат інтегрування. Якщо у підсумку дістанемо підінтегральну функцію, то інтеграл знайдено правильно. Отже, по таблиці похідних функції можна записати таблицю інтегралів.
Властивості невизначеного інтеграла:
1. 
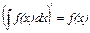
2. 
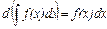
3. 
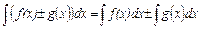
4. 
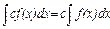
Таблиця невизначених інтегралів:
1. 
.
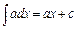2. 
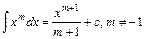. Зокрема, 
, 
, 
.
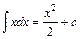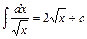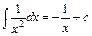3. 
.
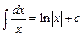4. 
.
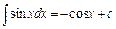5. 
.
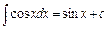6. 
.
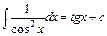7. 
.
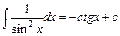8. 
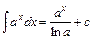. Зокрема 
.
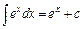9. 
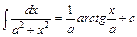. Зокрема, 
.
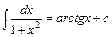10. 
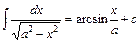. Зокрема, 
.
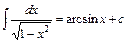11. 
.
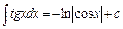12. 
.
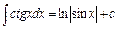13. 
.
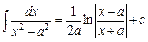14. 
.
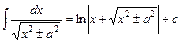Методи інтегрування:
· табличний – використовують табличні інтеграли, властивості інтегралів та властивості підінтегральної функції;
· заміни змінної під знаком інтеграла (метод підстановки) – полягає у використанні формули
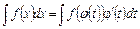, (2)
де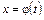 
, 
,
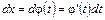або тієї ж формули у зворотному напрямку:
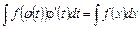, (2’)
де , .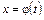
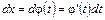Якщо функції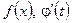 
неперервні, то рівності (2) і (2’) виконуються завжди. Заміна змінної є ефективною, якщо інтеграли справа у цих рівностях є простішим від відповідних інтегралів зліва. Якщо ж інтеграл справа ускладнився, то слід шукати іншу заміну, або відмовитись від цього методу інтегрування.
· інтегрування частинами – базується на використанні формули
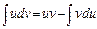, (3)
де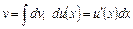 
.
У цій інтегральній тотожності підінтегральний вираз представлено у вигляді добутку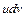 
. Якщо функції 
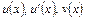є неперервними, тотожність (3) виконується завжди. Метод інтегрування частинами є ефективним лише у випадку, коли інтеграл справа у цій рівності 
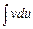є простішим за інтеграл зліва 
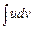. Якщо є інтеграл 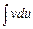став складнішим, то розбиття підінтегрального виразу на добуток 
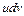і застосування формули (3) не приводить до результату. У цьому випадку слід позначити за u та dv інші частини підінтегрального виразу, або відмовитись від цього методу інтегрування.
Є функції, для інтегрування яких можна застосовувати наперед відомий метод інтегрування, а є такі, для інтегрування яких невідомо, який метод застосовувати. У цьому випадку застосовують один із перелічених методів. Не отримавши результату застосовують інший, або здійснюють перетворення над підінтегральною функцією і т.п.
