2015-08-13
604
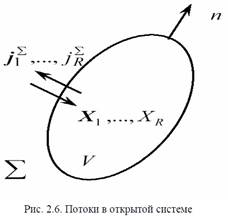
использованы уравнения баланса массы, дифференциальное уравнение Гиббса и полученное на их основе уравнение баланса энтропии и физический смысл используемых в этих уравнениях величин ясны из рис. 2.6.
Уравнение баланса массы:
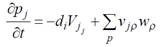(2.1)
Приведем также дифференциальное уравнение Гиббса
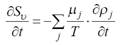(2.2)
где μj – химический потенциал единицы массы компонента
Xj, Sυ – плотность энтропии, функция ρj.
Для случая равновесия это уравнение имеет следующий вид:
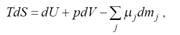(2.3)
где Т – температура;
U - внутренняя энергия; р – давление; m – масса.
На основе уравнений (2.1) и (2.2) может быть получено уравнение
баланса энтропии:
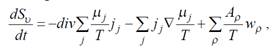(2.4)
С учетом полученных соотношений далее выводится теорема о ми-
нимальном производстве энтропии (Р). получаем следующее соотношение:
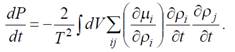
Учитывая произвольность вариаций концентраций ρi, вытекает неравенство
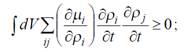
Тогда следует, что
dP / dt < 0 – вдали от стационарного состояния;
dP / dt = 0 – в стационарном состоянии.
Изменение производства энтропии во времени представлено на рис.2.7, что и является графической иллюстрацией теоремы о минимальном производстве энтропии, на основе которой делаются следующие утверждения.
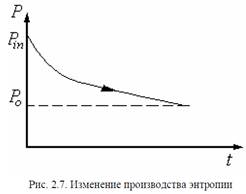В линейных системах выполняется общее неравенство, согласно которому в стационарном неравновесном состоянии производство энтропии имеет минимальное значение, зависящее от внешних условий, наложенных на систему.
При этом в системе могут иметь место возмущения либо внешней природы, обусловленные случайными или систематическими изменениями окружающей среды, либо внутренние флуктуации, возникающие в самой системе в результате межмолекулярного взаимодействия или случайного теплового движения частиц. В результате система непрерывно отклоняется на небольшую величину от макроскопического состояния, описываемого уравнениями баланса термодинамических переменных
