Рекурентна формула –це формула, що виражає загальний (n-й) член послідовності через попередні її члени; як-от: an = 2an-1+3an-2.
І нтеграл від найпростішого дробу IV-го типу шляхом повторного інтегрування частинами можна звести до інтегралу від найпростішого дробу III-го типу. Інтеграл від дробово-раціональної функції 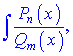 де
де 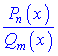 – правильний дріб, можна звести методом розкладу на доданки, які легко інтегруються за основними формулами інтегрування. Усі правильні раціональні дроби розкладаються на суму найпростіших раціональних дробів, коефіцієнти яких можна знайти методом невизначених коефіцієнтів. Кінцевий вигляд найпростіших дробів залежить від коренів знаменника
– правильний дріб, можна звести методом розкладу на доданки, які легко інтегруються за основними формулами інтегрування. Усі правильні раціональні дроби розкладаються на суму найпростіших раціональних дробів, коефіцієнти яких можна знайти методом невизначених коефіцієнтів. Кінцевий вигляд найпростіших дробів залежить від коренів знаменника 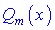 та їх кратності.
та їх кратності.
7. розклад правильного раціонального дробу на суму простіших елементарнихІнтегрування правильного раціонального дробу 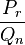 , r < n, за допомогою розкладу в суму найпростіших дробів зводиться до інтегрування дробів вигляду
, r < n, за допомогою розкладу в суму найпростіших дробів зводиться до інтегрування дробів вигляду 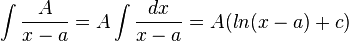 ,
,
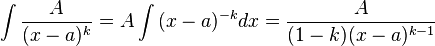 ,
,
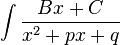 ,
,
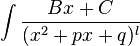
де {k,l}  {2,3,...}; А,В,С,а,р,q - сталі, причому
{2,3,...}; А,В,С,а,р,q - сталі, причому 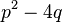 < 0.
< 0.
8. Метод невизначених коефіцієнтів Якщо лінійне диференціальне рівняння є рівнянням з сталими коефіцієнтами, а функція 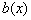 спеціального виду, то частинний розв’язок можна знайти за допомогою методу невизначених коефіцієнтів.1) Нехай
спеціального виду, то частинний розв’язок можна знайти за допомогою методу невизначених коефіцієнтів.1) Нехай 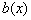 має вид многочлена, тобто
має вид многочлена, тобто
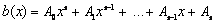 .
.
а) Розглянемо випадок, коли характеристичне рівняння не має нульового кореня, тобто 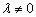 . Частинний розв’язок неоднорідного рівняння шукаємо вигляді:
. Частинний розв’язок неоднорідного рівняння шукаємо вигляді:
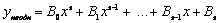 ,
,
де 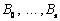 - невідомі сталі. Тоді
- невідомі сталі. Тоді
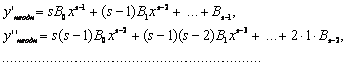
Підставляючи у вихідне диференціальне рівняння, одержимо
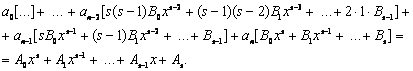
Прирівнявши коефіцієнти при однакових степенях 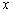 запишемо:
запишемо:

Оскільки характеристичне рівняння не має нульового кореня, то 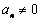 . Звідси одержимо
. Звідси одержимо
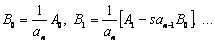 .
.
10. Інтеграли від ірраціональних функцій
Не від всякої ірраціональної функції інтеграл виражається через елементарні функції. Зараз ми розглянемо ті ірраціональні функції, інтеграли від яких за допомогою підстановок приводяться до інтегралів від раціональних функцій і, отже, до кінця інтегруються.
1.Розглянемо інтеграл 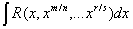 , Де R-раціональна функція своїх аргументів [1]).
, Де R-раціональна функція своїх аргументів [1]).
Нехай R-загальний знаменник дробів m / n,... r / s. Зробимо підстановку 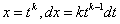 . Тоді кожна дробова ступінь х виразиться через цілу ступінь t і, отже, підінтегральна функція перетворюється в раціональну функцію від t.
. Тоді кожна дробова ступінь х виразиться через цілу ступінь t і, отже, підінтегральна функція перетворюється в раціональну функцію від t.
11. Знаходження інтегралів типу 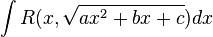 , де R раціональна функція двох змінних, проводиться за допомогою тригонометричних підстановок таким чином. За допомогою виділення повного квадрата в квадратному тричлені і наступної заміни
, де R раціональна функція двох змінних, проводиться за допомогою тригонометричних підстановок таким чином. За допомогою виділення повного квадрата в квадратному тричлені і наступної заміни 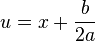 вихідний інтеграл зводиться до інтеграла одного з таких трьох типів:
вихідний інтеграл зводиться до інтеграла одного з таких трьох типів:
1) 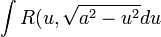
2) 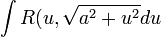
3) 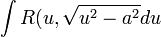 .
.
12, (перша підстановка Ейлера). Якщо 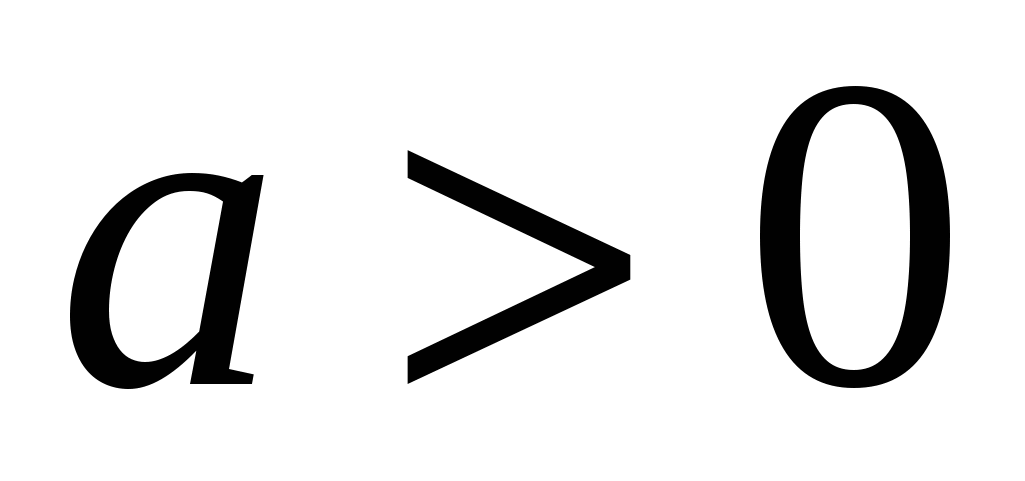 , тоді використовується підстановка:
, тоді використовується підстановка:
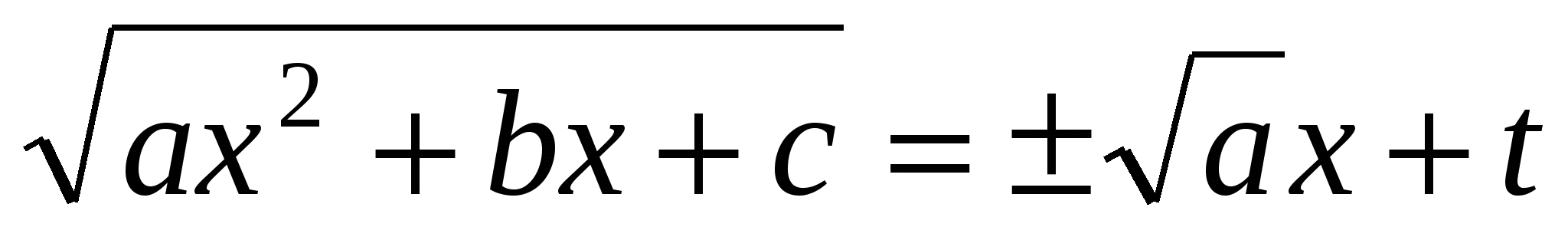
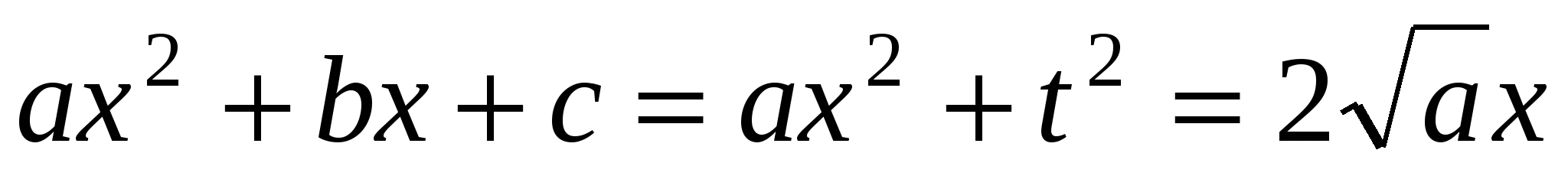

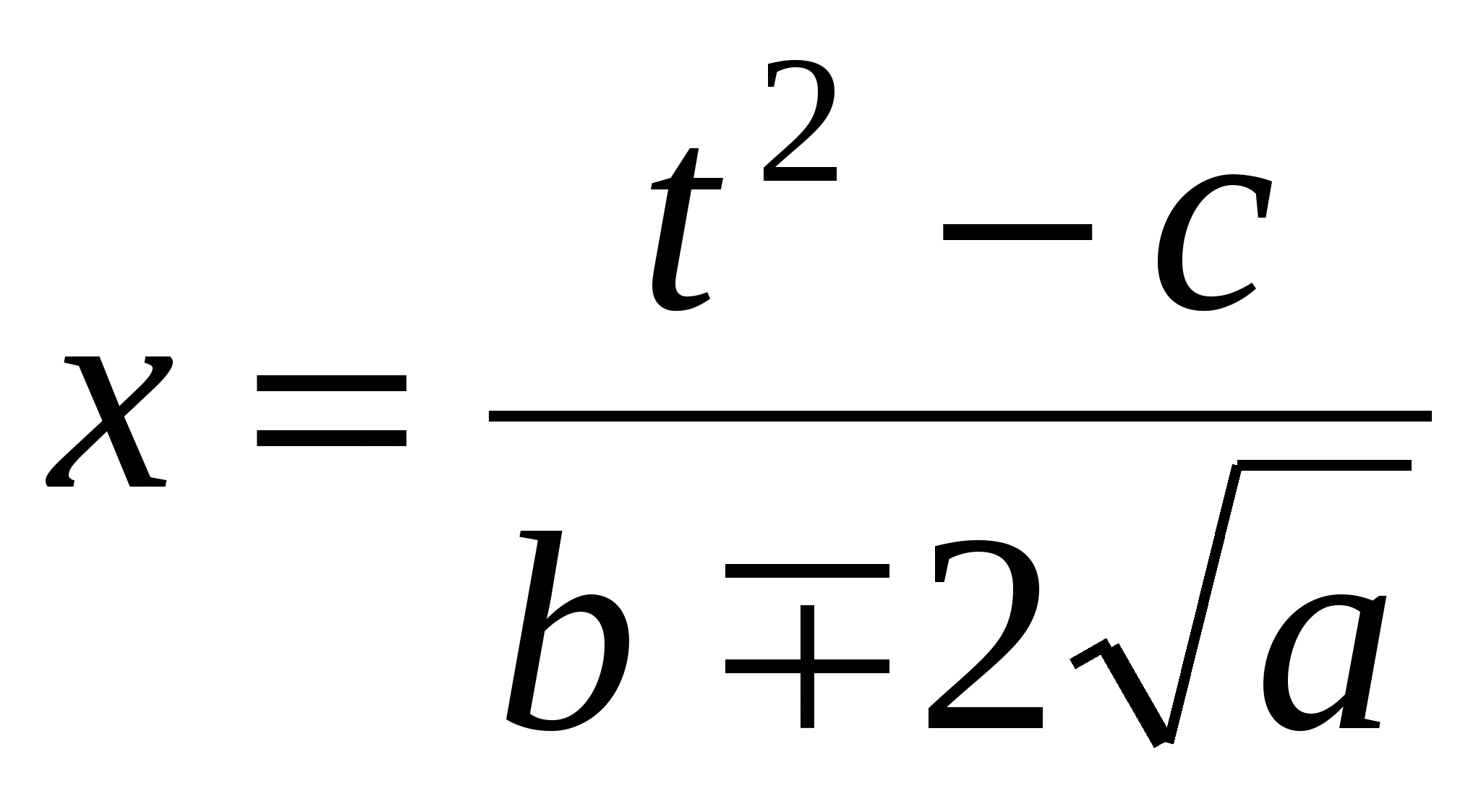
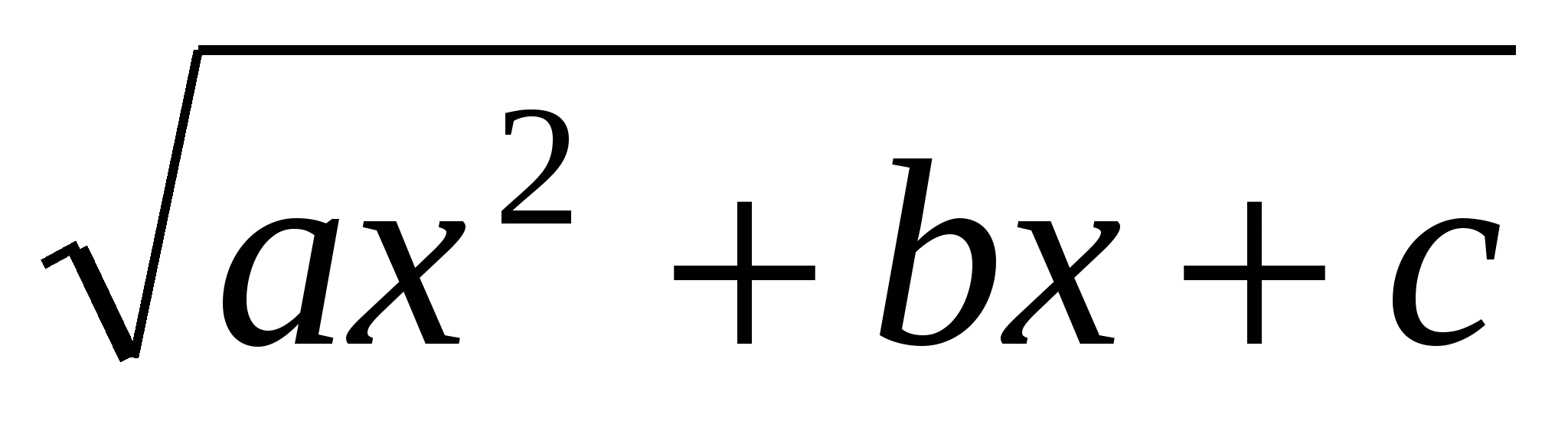 і
і 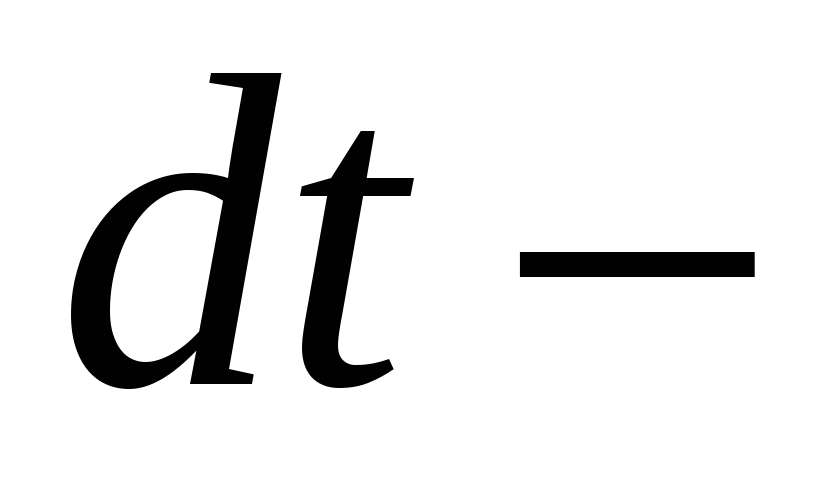 раціональні вирази.
раціональні вирази.
13. Якщо 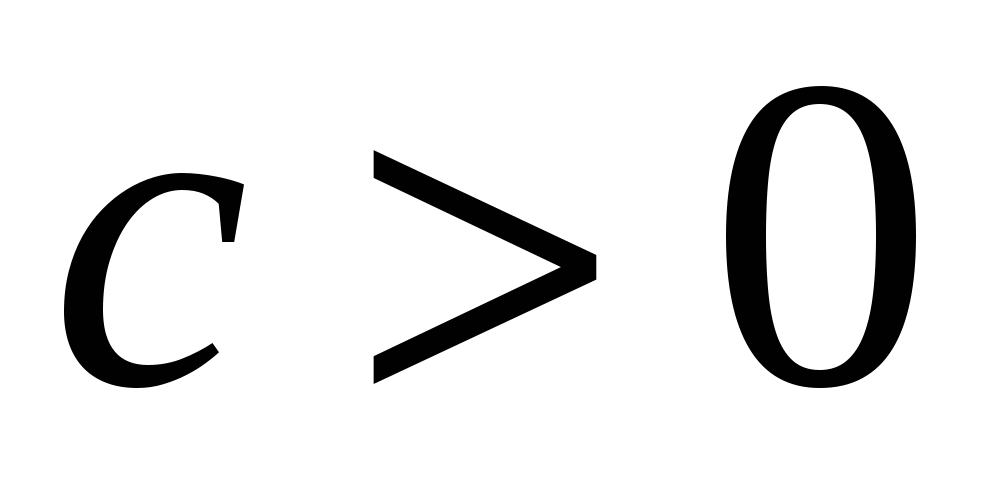 , тоді (друга підстановка Ейлера)
, тоді (друга підстановка Ейлера)
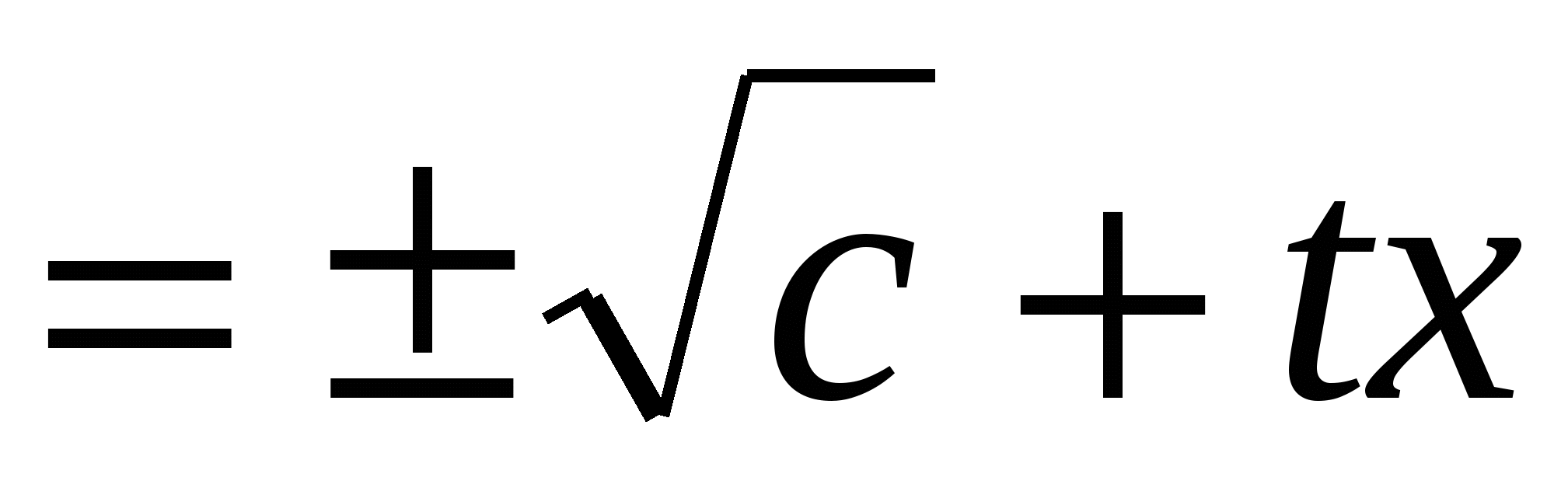 і аналогічно першій.
і аналогічно першій.
14.Якщо 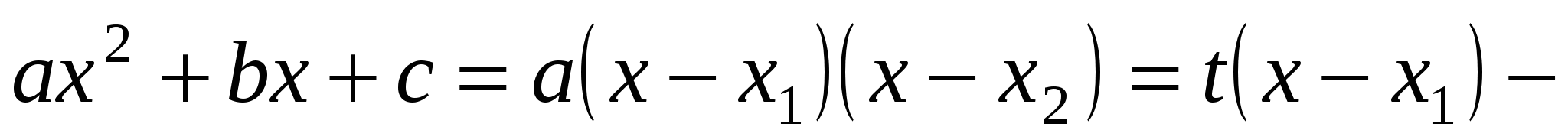 (третя підстановка Ейлера).
(третя підстановка Ейлера).
 2015-08-13
2015-08-13 1522
1522







