Определение 1. Многочленом (полиномом) называется сумма степенных функций с целыми положительными показателями степеней и с постоянными коэффициентами при этих функциях.
Определение 2. Степенью многочлена называют старшую степень функции, входящей в многочлен.
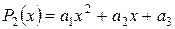 ,
, 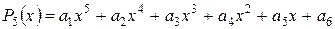 .
.
Выше приведены обозначения многочленов второй и пятой степеней, 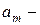 постоянные коэффициенты при степенных функциях.
постоянные коэффициенты при степенных функциях.
Определение 3. Корнем многочлена называют число, обращающее многочлен в нуль. Если все корни многочлена различные, говорят, что у многочлена простые корни. Если многочлен имеет несколько одинаковых корней, говорят, что многочлен имеет кратные корни. Когда говорят, что  корень пятой кратности, имеют ввиду, что у многочлена пять одинаковых корней
корень пятой кратности, имеют ввиду, что у многочлена пять одинаковых корней  .
.
Как уже говорилось выше, многочлен может не иметь корней на множестве действительных чисел, но на множестве комплексных чисел он всегда имеет корни простые или кратные, причем их число равно степени многочлена.
Примеры.
1. 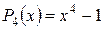 . Это неполный многочлен четвертой степени, (присутствуют не все степени
. Это неполный многочлен четвертой степени, (присутствуют не все степени  ). Преобразуем многочлен
). Преобразуем многочлен
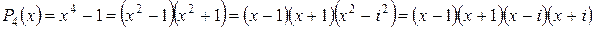
Ясно, что на множестве действительных чисел этот многочлен имеет два корня 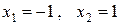 , на множестве комплексных чисел у него четыре простых корня
, на множестве комплексных чисел у него четыре простых корня 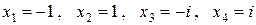 (два действительных и два чисто мнимых).
(два действительных и два чисто мнимых).
2. 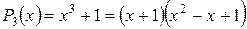 - неполный многочлен третьей степени.
- неполный многочлен третьей степени.
Решим уравнение
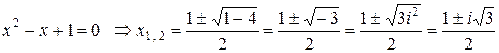 .
.
Итак, на множестве комплексных чисел имеем три корня 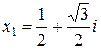 ,
,
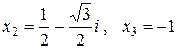 , один из них действительный.
, один из них действительный.
Теорема 1.
Если 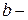 корень многочлена
корень многочлена 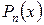 , то есть
, то есть 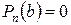 , то многочлен делится нацело на выражение
, то многочлен делится нацело на выражение 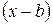 . Другими словами,
. Другими словами, 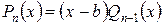 .
.
Доказательство.
Предположим, что многочлен 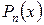 делится на
делится на 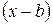 с остатком, то есть
с остатком, то есть
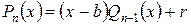 . Очевидно,
. Очевидно, 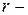 постоянная, ибо в противном случае следует продолжать деление. Подсчитаем
постоянная, ибо в противном случае следует продолжать деление. Подсчитаем 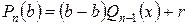 . Поскольку
. Поскольку 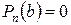 , равенство возможно лишь при
, равенство возможно лишь при 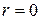 , что и требовалось доказать.
, что и требовалось доказать.
Следствие. Если 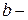 корень многочлена кратности
корень многочлена кратности 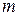 , то
, то 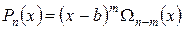 , причем
, причем 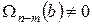 .
.
Теорема 2.
Если многочлен с действительными коэффициентами имеет комплексный корень, то он имеет и комплексно сопряженный корень той же кратности.
Доказательство. Дан многочлен
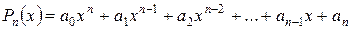 ,
,
все коэффициенты которого 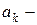 действительные, причем
действительные, причем 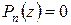 , а
, а 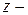 комплексное число. Докажем, что комплексно сопряженное число
комплексное число. Докажем, что комплексно сопряженное число 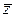 также является корнем многочлена. Итак,
также является корнем многочлена. Итак,
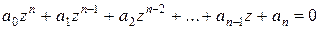 .
.
Поскольку 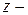 комплексное число, сумма и степень комплексного числа есть комплексное число, левая часть равенства представляет собой комплексное число, причем равное нулю. При изучении комплексных чисел было установлено, что комплексное число равняется нулю только в том случае, если его действительная и мнимая части равны нулю. Но тогда равно нулю и комплексно сопряженное число
комплексное число, сумма и степень комплексного числа есть комплексное число, левая часть равенства представляет собой комплексное число, причем равное нулю. При изучении комплексных чисел было установлено, что комплексное число равняется нулю только в том случае, если его действительная и мнимая части равны нулю. Но тогда равно нулю и комплексно сопряженное число
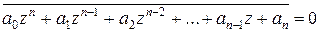 ,
,
Ранее было доказано, что комплексное число от суммы равно сумме комплексных чисел, тогда
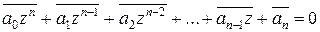 .
.
Так как произведение комплексно сопряженных чисел равно комплексно сопряженному от их произведения, а все 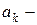 действительные,
действительные,
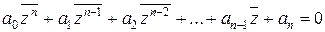 .
.
Наконец, 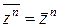 , откуда следует
, откуда следует
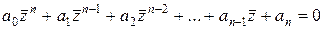 .
.
Теорема доказана.
Следствие 1. Если у многочлена с действительными коэффициентами 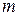 одинаковых комплексных корней
одинаковых комплексных корней 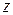 , то он имеет также
, то он имеет также 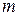 комплексно сопряженных корней
комплексно сопряженных корней 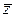 .
.
Теорема 3. Если многочлен 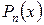 с действительными коэффициентами имеет
с действительными коэффициентами имеет 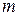 одинаковых комплексных корней
одинаковых комплексных корней 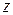 , то он может быть представлен в виде
, то он может быть представлен в виде
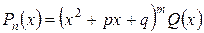 ,
,
причем 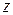 и
и 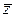 - корни многочлена
- корни многочлена 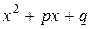 , а
, а 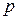 и
и 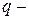 действительные числа.
действительные числа.
Доказательство. Многочлен с действительными коэффициентами в соответствии с предыдущим следствием имеет 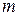 пар комплексно сопряженных корней
пар комплексно сопряженных корней 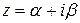 ,
, 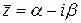 . Тогда из следствия теоремы 1
. Тогда из следствия теоремы 1
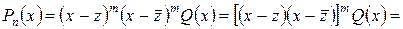
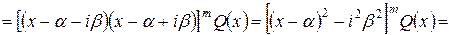
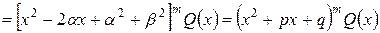 ,
,
здесь 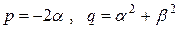 .
.
 2015-08-13
2015-08-13 13723
13723