Теоретические сведения

Задание

Аппроксимировать табличные значения (таблица 1) методом наименьших квадратов полиномами 1, 2, и 4 степеней.

Таблица 1

X	Y
-1.0	7.75
-0.5	6.7
	5.45
0.5
	2.35

Теоретические сведения

Пусть дана таблица значений функции 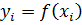в узлах 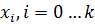, где 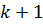- количество узлов:

Таблица 2

№
…	…	…
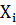
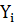
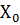
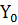
k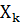

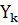
Необходимо определить коэффициенты аппроксимирующего полинома 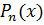порядка n

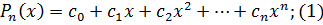
из условий:

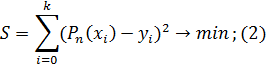
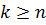
В узлах 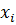между значениями полинома 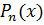и функции 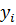будет разность, называемая отклонением. Если выбрать порядок полинома 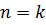, то получим полином, совпадающий с интерполяционным. Аппроксимирующая кривая в этом случае пройдёт точно через точки таблицы, и величина 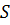будет равна нулю.

Подставляя в (2) выражение для полинома (1), получим:

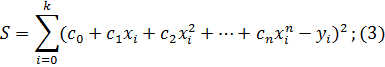
Значения 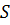зависят от коэффициентов 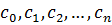, т. е. 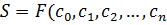). Коэффициенты полинома определяются из условия минимума функции :

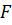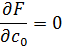
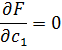
... … … … (4)

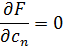
После преобразований (4) получим систему алгебраических уравнений:

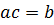; (5)

где с – неизвестные коэффициенты полинома; а – матрица коэффициентов; b – вектор правой части системы уравнений.

Пусть 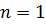, тогда система (5) будет выглядеть следующим образом:

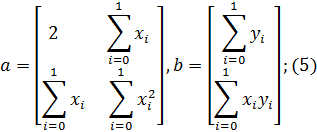
Значения полинома в точке x вычисляются по схеме Горнера:

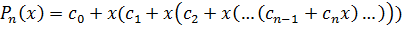; (7)

Рассмотрим в качестве примера расчёт трёхточечного задания (табл. 3):

Таблица 3

i	X	Y
	-1	7.75
		5.45
		2.35

Полином первого порядка примет вид: 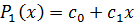. Коэффициенты полинома определяются из условия

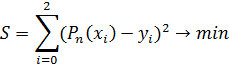
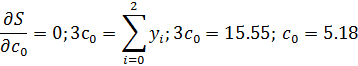
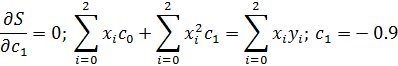
Искомый полином запишется в виде: 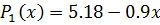. На рис. 1 представлены исходные данные и аппроксимирующий полином.

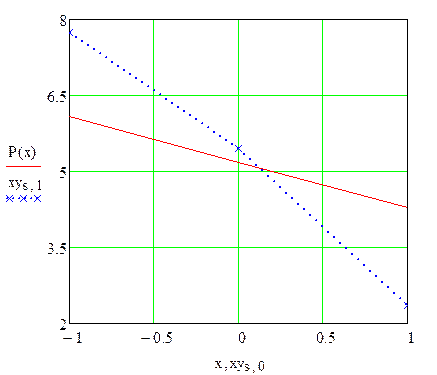Рисунок 1. График исходных данных и полинома.