Решение

Основываясь на положениях теории РЦ, определим погрешность базирования для размера 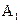. Из размерной цепи (рис.2), звеньями которой являются размеры 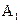, , 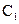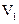(причем размер 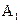выступает в качестве замыкающего звена этой цепи), следует:

= + ,

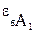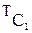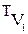где V₁ – технологический размер измерительной базы выдерживаемого размера 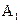– размер, определяющий положение измерительной базы выдерживаемого размера (ИБ (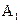)) относительно его технологической базы (ТБ (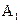)) в направлении выдерживаемого размера,

С₁ – технологический размер конструктивного элемента выдерживаемого размера 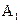– размер, определяющий положение конструктивного элемента выдерживаемого размера (КЭ (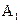)) по отношению к его технологической базе (ТБ (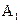)) в направлении выдерживаемого размера.

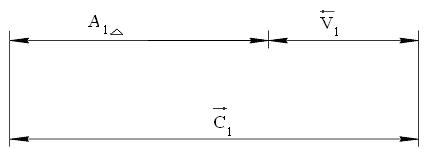
Рисунок 2. Расчетная схема размерной цепи

Поскольку каждый 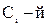размер будет определять взаимное положение соответствующих ему двух элементов, которые у всех обработанных заготовок партии будут занимать одинаковое и строго определенное взаимное положение, то поле рассеяния такого размера, которое можно истолковывать как его допуск, будет равно нулю, т.е.:

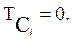(1)

C учетом соотношения [1]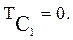

Тогда:

= .

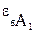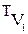Решим задачу геометрически (рис. 1б). Так, на рис. 1б ИБ (А₁) займет крайнее левое положение, когда на обработку поступит заготовка с размером S₄ =S_4max, и крайнее правое – при S₄ =S_4min=0, это обусловит колебание размера A₁ в пределах от A_1min до A_1max. Погрешность базирования равна:

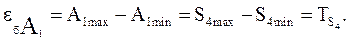
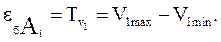
По рисунку 1б находим:

V_1min=0.

Найдем V_1max. Он будет достигаться при S_4max. Рассмотрим треугольники OBC и ODF. Из подобия треугольников:

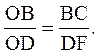
Подставим размеры (из таблицы 1):

V_1max=(S_4max(S₁-H))/S₁=0,12(48-24)/48=0,06 мм

V_1min=(S_4min(S₁-H))/S₁=0(48-24)/48=0мм

Найдем погрешность базирования выдерживаемого размера А₁:

ε_бА1= V_1max - V_1min=0,06-0=0,06 мм

Допуск на размер А₁ (из таблицы 1):

T_V1=0,140 мм.

Требуемая точность обработки обеспечивается.

Основываясь на положениях теории РЦ, определим погрешность базирования для размера 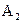. Из размерной цепи (рис. 3), звеньями которой являются размеры 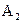, , 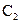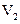следует:

= + .

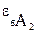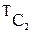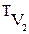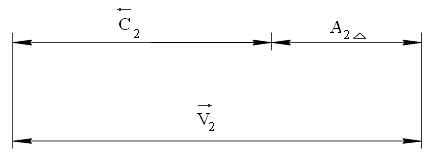
Рисунок 3. Расчетная схема размерной цепи

Учитывая [1]:

= .

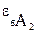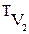С учетом тождественности размеров V₂ и S₁:

= .

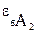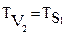Допуск на размер S₁ (из таблицы 1):

ε_бА2=Т_S1=0,160 мм

Решим задачу геометрически (рис. 1б). Так, на рис. 1б ИБ (А₂) займет крайнее верхнее положение, когда на обработку поступит заготовка с размером S₁ =S_1max, и крайнее нижнее – при S₁ =S_1min, это обусловит колебание размера A₂ в пределах от A_2min до A_2max. Погрешность базирования равна:

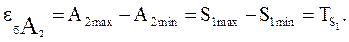
Допуск на размер A₂ (из таблицы 1):

Т_А2=0,360 мм

Требуемая точность обработки обеспечивается.