Симплекс метод
Симплекс - метод – это ряд шагов, заключающихся в том, что от данного базиса мы переходи к другому базису так, чтобы значение F увеличилось или по крайней мере не уменьшилось.
Если в жордановой таблице дописать строку для целевой функции, то полученная таблица будет называться симплексной.
Последовательность решения задачи симплекс методом
1. Исходную систему ограничения приведем к виду, когда свободные члены не отрицательны. Для этого умножим на минус 1 ограничения, имеющие отрицательный свободный член.
2. Если дана задача на отыскание min, то переменой знака целевой функции на противоположный ее сводят к задаче на max.
3. Задача должны быть записана в канонической форме.
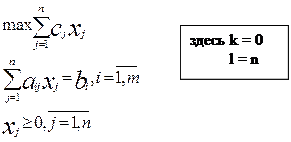 |
4. Составим симплекс таблицу. (Функция цели записывается с обратным знаком, кроме свободного члена).
5. Найдем начальный опорный план по правилу:
v среди положительных чисел основной части таблицы выберем то, для которого имеет место минимальное симплексное отношение:
min = свободный член / положительный элемент разрешающего столбца
В качестве разрешающего столбца можно выбрать тот, в котором
- в F - строке стоит 0 или столбец, содержащий положительный элемент (в других столбцах такого нет).
- разрешающий столбец выбирается любой, где есть положительный элемент
Если исходную таблицу преобразовать с различными исходными разрешающими элементами, получим другой опорный план и базисное решение.
v выполним шаг жорданова исключения (пока не сформирован базис);
v жордановых исключений осуществляем столько, сколько переменных необходимо ввести в базис, пока не заполнится столбец базисных переменных;
v искомое опорное решение находим, приравняв (верхнее) свободные переменные 0, а (боковые) базисные свободным членам;
v если в ходе жордановых исключений встретится 0-я строка, в которой все элементы нули, а свободный член не отрицателен, то данная система не имеет не отрицательных (в частности опорных) решений, хотя и является совместной;
v если 0-строка, а свободный член не 0, то решение не имеет.
v полученный опорный план исследуется на оптимальность.
Оптимальный план может быть:
- единственным
- бесконечное множество
Опорный план может указывать на
- неразрешимость задачи
- возможность улучшить план
С этой целью исследуется целевая функция по следующему правилу:
- если в строке целевой функции нет отрицательных элементов не считая свободного элемента, то план оптимален;
- если в строке целевой функции нет отрицательных элементов и нет 0-х элементов, то оптимальный план единственный;
- если среди положительных элементов F-строки есть хотя бы один 0-й элемент, то оптимальных планов бесконечное множество;
- если в F-строке есть хотя бы один отрицательный элемент, а в соответствующем столбце нет положительных, то целевая функция не ограничена в допустимой области (F→∞). Задача неразрешима.
- если в F-строке есть хотя бы один отрицательный элемент, а в каждом столбце с таким элементом есть хотя бы один положительный, то можно перейти к новому опорному плану, более близкому к оптимальному.
v для улучшения опорного плана столбец с отрицательным элементом в F-строке берут за разрешающий, если в F-строке отрицательных элементов несколько, то выбирают столбец с наибольшим по абсолютной величине отрицательным элементом. Далее по минимальному симплексному отношению определяют разрешающую строку и делают шаг жордановых исключений, полученный план опять исследуют на оптимальность и т.д.
Если в базисном решении есть отрицательная переменная, то это решение для задачи ЛП является недопустимым.
Пример. Найти оптимальный опорный план
F = 3х1 - х2 + 5 → max
х1 + х2 - х3 - х4 = - 4 (1)
х1 - 2х2 - х3 - х5 = -7 (2)
2х1 - х2 + х4 + х5 = 7 (3)
 xj ≥ 0, j=1,5
xj ≥ 0, j=1,5
1. В уравнениях (1) и (2) необходимо избавиться от отрицательного свободного члена, умножив каждое на (-1):
F = 3х1 - х2 + 5 → max
- х1 - х2 + х3 + х4 = 4
- х1 + 2х2 + х3 + х5 = 7
2х1 - х2 + х4 + х5 = 7
 xj ≥ 0, j=1,5
xj ≥ 0, j=1,5
| - х1 | -х2 | -х3 | - х4 | - х5 | ||
| -1 | -1 | |||||
| -1 | ||||||
| -1 | ||||||
| F | -3 |
| - х1 | -х2 | -х3 | - х5 | ||
| х4 | -1 | -1 | |||
| -1 | |||||
| -1 | |||||
| F | -3 |
| - х1 | -х2 | -х3 | ||
| х4 | -1 | -1 | ||
| -4 | ||||
| х5 | -1 | |||
| F | -3 |
| - х1 | -х2 | ||
| х4 | -2 | ||
| х3 | -2 | ||
| х5 | |||
| F | -3 |
В левом столбце последней таблицы нет нулей, значит базис выделен. Ему соответствует начальный опорный план: хопорный = (0, 0, 2, 2, 5)
F = 3*0 – 0 + 5=5
Если исходную таблицу преобразовать с другими разрешающими элементами, то получим другой базис и, следовательно, другой оптимальный план.
Найденный опорный план не оптимален, т.к. в F – строке есть отрицательный элемент (-3). В соответствующем ему столбце имеются положительные элементы, поэтому есть возможность улучшить план.
Для получения нового опорного плана в последней таблице выбирают разрешающий элемент;
- столбец с элементом (-3),
- строку по минимальному симплексному отношению: min (2/1, 5/1).
| - х4 | -х5 | ||
| х1 | |||
| х3 | |||
| х2 | |||
| F | 4/3 | 5/3 |
| - х4 | -х2 | ||||
| х1 |
| ||||
| х3 | -3 | ||||
| х5 | -1 | ||||
| F | -5 |
|
хпорный = (2, 0, 6, 0, 3) План оптимальный и единственный
Пересчитана строка функции цели
F = 3*2 – 0 + 5=11
хopt = (4, 1, 9, 0, 0) Fmax = 3*4 – 1 + 5=16
 2015-08-21
2015-08-21 1276
1276