1. Составить первую симплекс-таблицу.
2. Проверить опорное решение на оптимальность.
Если в индексной строке все оценки неположительные, то опорное решение оптимально, а значение 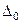 – наименьшее значение целевой функции на допустимом множестве.
– наименьшее значение целевой функции на допустимом множестве.
3. Проверить задачу на неограниченность.
Если в индексной строке содержится положительная оценка, над которой в таблице нет ни одного положительного элемента, то целевая функция не ограничена снизу на допустимом множестве и задача не имеет решения.
4. Выбрать ведущий элемент, выполнить жорданово исключение и заполнить следующую симплекс-таблицу.
С полученной таблицей возвращаемся к пункту 2.
Пример. Решить задачу 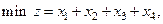
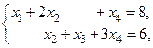
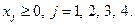
Решение. Решение запишем в виде последовательности таблиц.
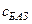
| Базис | 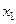
| 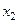
| 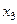
| 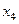
| В |
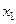
| 
| |||||
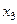
| ||||||
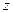
| ||||||
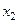
| 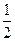
| 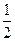
| ||||
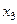
| 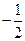
| 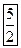
| ||||
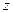
| –1 | |||||
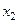
| 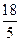
| |||||
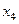
| 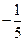
| 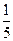
| 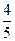
| |||
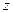
| 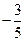
| 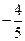
| 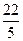
|
Ответ. 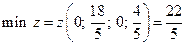 .
.
Пример. Решить задачу 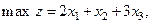
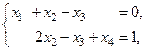
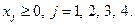
Решение. Приведем задачу к каноническому виду:
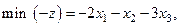
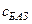
| Базис | 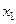
| 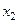
| 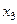
| 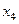
| В |
| –2 | –1 | –3 | ||||
| –2 | 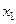
| –1 | ||||
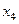
| –1 | |||||
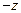
| –1 |
Ответ. 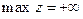 .
.
 2015-08-21
2015-08-21 314
314







