2015-08-21
320
СИМПЛЕКС-МЕТОД РЕШЕНИЯ
Базисным решением системы линейных уравнений с единичным базисом называется частное решение, в котором значения свободных переменных равны нулю. Если все координаты базисного решения неотрицательны, то оно называется опорным решением.
Например, для системы
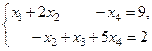
базисным и опорным решением является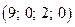 
.
Пусть дана задача линейного программирования в канонической форме, система ограничений которой является системой с единичным базисом и правые части всех уравнений неотрицательны.
,
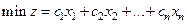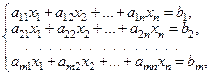
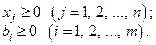
Обозначим базисные переменные, входящие в первое, …,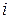 
-е, …, последнее уравнения через
, …, 
, …, 
,
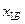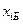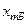соответственно, а коэффициенты при этих переменных в целевой функции –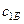 
, …, 
, …, 
.
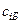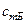Данные задачи запишем в виде таблицы. Она называется первой симплекс-таблицей.
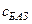
| Базис |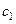 
| … | 
| … | 
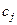
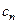
| В |
| … | 
| … | 
| |||
|
|
| 
| … | 
| … | 
| 
|
| … | … | … | … | … | … | … | … |
|
|
| 
| … | 
| … | 
| 
|
| … | … | … | … | … | … | … | … |
|
|
| 
| … | 
| … | 
| 
|
| 
| … | 
| … | 
| 
|
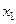
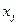
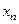
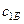
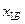
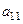
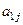
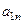
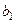
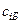
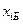
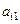
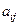
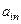
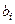
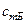
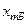
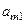
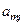
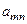
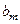
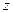
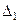
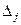
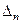
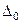
Последняя строка таблицы называется индексной строкой. Числа 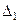, …, , …, 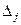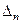называются оценками переменных 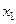, …, , …, 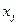, 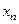соответственно. Вычисляются оценки по формулам
|
|
|
, …,
,…,
.
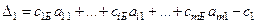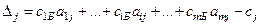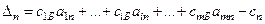Оценки, соответствующие базисным переменным, равны нулю.
Число 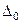равно значению целевой функции 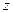на опорном решении, соответствующем базису , …, , …, .
.
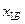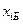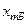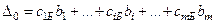Остальные симплексные таблицы, возникающие в процессе решения задачи симплекс-методом, имеют ту же структуру, что и первая таблица, но при их составлении можно отбросить шапку таблицы и первый столбец.
Пример. Для задачи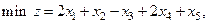 
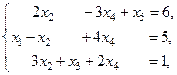
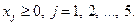
составить первую симплексную таблицу.
Решение. Базисные переменные в этой системе: ,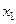 
, 
.
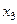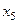Опорное решение: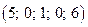 
.
|
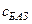
| Базис |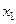
| 
|
| 
|
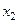
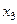
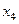
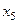
| В |
| –1 | |||||||
|
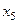
| –3 | ||||||
|
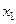
| –1 | ||||||
| –1 |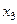
| ||||||
|
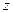
| – 4 |
