Terminate 1

Нужно найти такое значение параметра NWorkers, при котором доход достигал бы максимального значения. В выражение дохода PRIBY входит количество изготовленных изделий, равное значению СЧА N$OUT. Понятно, что доход может быть как отрицательным (убытки от производства), так и положительным (когда производство становится прибыльным).

Диалоговое окно эксперимента заполним, как показано на рис. 9.15. Используем ту же процедуру DoTheRun, что и в примере 9.5.

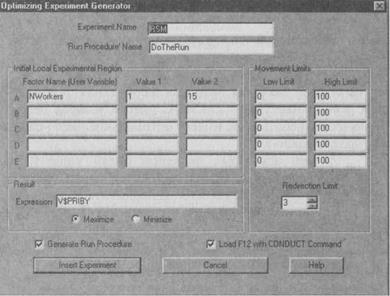
Рис. 9.15

02/15/03 20:27:35 CONDUCT RSM()

02/15/03 20:27:35 **** Experiment in Progress. ****

02/15/03 20:27:35 Simulation in Progress.

02/15/03 20:27:35 A Simulation in an Experiment has ended. Clock is
2400.000000.

02/15/03 20:27:35 "Run 1. Yield=-235. NWorkers=l;"

02/15/03 20:27:35 Simulation in Progress.

02/15/03 20:27:35 A Simulation in an Experiment has ended. Clock is
2400.000000.

02/15/03 20:27:35 "Run 2. Yield=-1185. NWorkers = 15; "

02/15/03 20:27:36 Simulation in Progress.

)2/15/03 20:27:36 A Simulation in an Experiment has ended. Clock is
2400.000000'.

02/15/03 20:27:36 "Run 3. Yield=-130. NWorkers=8;"

02/15/03 20:27:36 Simulation in Progress.

2/15/03 20:27:36 A Simulation in an Experiment has ended. Clock is
2400.000000.

02/15/03 20:27:36 "Run 4. Yield=-120. NWorkers=8;"

02/15/03 20:27:36 Simulation in Progress.,

02/15/03 20:27:36 A Simulation in an Experiment has ended. Clock is
2400.000000.

02/15/03 20:27:36 "Run 5. Yield=-140. NWorkers=8;"

02/15/03 20:27:36 Using Model:

02/15/03 20:27:36 Y - -344.694 +121.531 A -11.8367 A»2

02/15/03 20:27:36 Predicted optimum yield is -32.7478.

02/15/03 20:27:36 Optimum is in the local Experimental Region.

02/15/03 20:27:36 RSM_FitSurfaceToData() returns 4.

02/15/03 20:27:36 "Running the predicted Optimum."

02/15/03 20:27:36 Simulation in Progress.

02/15/03 20:27:36 A Simulation in an Experiment has ended. Clock is
2400.000000.

02/15/03 20:27:37 "Run 6. Yield=254.9568965517241. NWork-

ers=5.133620689655173;'

02/15/03 20:27:37 Experiment ended.

Таким образом, получен следующий результат: в процессе поис­ка решения была построена модель второго порядка

Y =-344.694+ 121.531А- 11.8367А².

Оптимальные значения: входная переменная NWorkers=5.13, выходная переменная Yield = 254.96. С учетом условия целочисленности количества работников, имеем: оптимальное число работников для этой модели равно 5.

При некоторых значениях полей Value I, Value 2 диалогового окна Optimizing Experiment Generator процедура оптимизирующего эксперимента не выполняет по­следний прогон «Running the predicted Optimum» и не вы­дает искомый результат. Также может быть выдано такое сообщение «Goodness of fit test fails. Standard Error is 0. Cannot perform F test". В этих случаях нужно изменить значения Value 1 и Value 2.

Эксперименты пользователя. Пользовательский эксперимент в GPSS World - очень гибкий и мощный инструмент, так как с помо­щью встроенного языка PLUS можно задать выполнение разнообраз­ных, достаточно сложных действий. Кроме того, выполняющийся эксперимент позволяет вызывать любые команды GPSS из процедур на языке PLUS. Подпрограммы на языке PLUS делятся на процедуры (в заголовке используется ключевое слово PROCEDURE) и экспери­менты (EXPERIMENT) Эти подпрограммы должны находиться в файле модели. Разница между этими двумя видами подпрограмм за­ключается в следующем. Процедуры с помощью оператора RETURN могут возвращать значение, которое можно посмотреть с помощью команды SHOW, либо использовать в других подпрограммах. Для этого сначала нужно оттранслировать модель вместе с процедурой или же просто процедуру, если модель не используется. При этом процедура регистрируется. Затем в меню нужно выбрать пункт Command/SHOW и написать там название процедуры, указав в скобках нужные параметры или ничего не указывая (если параметров нет). После этого процедура выполняется и выдается результат.

Процедуры на языке PLUS также могут использоваться в коман­дах GPSS в качестве операндов. В этом случае они заключаются в круглые скобки. Эти процедуры, в свою очередь, в качестве парамет­ров могут использовать вызовы других процедур. Это очень мощное новшество GPSS World значительно повышает возможности и гиб­кость модели.

Эксперимент отличается от процедуры тем, что он может быть вызван (выполнен) только пользователем. Для этого нужно выбрать пункт меню Command/CONDUCT и написать там название экспе­римента, указав в круглых скобках параметры, если они имеются, или ничего не указывая, если параметров нет. Что нового дает экспери­мент? Ключевым моментом является то, что с помощью библиотеч­ной процедуры DoCommand можно вызывать любую команду GPSS, а это позволяет многократно выполнять прогоны модели и в каждом прогоне получать доступ к текущим результатам. Из подпрограммы эксперимента могут вызываться процедуры, которые в свою очередь могут вызывать другие процедуры и т.д. Причем из любой процеду­ры, на какой бы глубине вложенности вызовов она ни была, можно вызывать процедуру DoCommand. Поэтому структура выполняемого кода эксперимента может быть какой угодно сложной. Таким обра­зом, пользовательский эксперимент объединяет в себе набор проце­дур на языке PLUS, в котором одна из процедур имеет в заголовке ключевое слово EXPERIMENT. Выполнить такой эксперимент мож­но с помощью команды CONDUCT. Разные эксперименты могут иметь общие вызываемые процедуры.

В пользовательском эксперименте для задания последователь­ности команд и исходных данных каждого прогона модели удобно использовать PLUS-процедуру. Такая процедура может инициализи­ровать генераторы случайных чисел, выполнять команды и управлять имитацией.

В руководстве по GPSS World пользовательские эксперименты используются исключительно с процедурой ANOVA, однако, их можно использовать для решения совершенно разных задач. Рас­смотрим несколько практических примеров пользовательского экспе­римента.

В этих задачах нужно найти значения параметров системы, при которых ее критерий эффективности достигает оптимума. Алгоритм поиска решения базируется на том, что экономические показатели реальных систем обычно представляют собой функции, имеющие единственный локальный экстремум, который и является глобаль­ным.

Рассмотрим еще раз задачу из примера 9.6. Использование в этом примере оптимизирующего эксперимента было не совсем кор­ректным. Оптимизирующий эксперимент рассчитан на модели, рабо­тающие в стационарном режиме, а для данного примера нет гарантий, что за пять дней работы моделируемая система войдет в такой режим.

Поэтому следует считать, что система работает в переходном режиме, и для каждого значения количества работников необходимо провести некоторое число прогонов модели.

Воспользуемся программой из примера 9.6 и организуем для этой модели пользовательский эксперимент, но прежде рассмотрим алгоритм поиска оптимума. Предполагаем, что целевая функция, оп­ределяющая прибыль, имеет единственный оптимум. Если бы време­на сборки и обработки детали на машине были бы детерминирован­ными, то оптимальное количество работников находилось бы вблизи величины, равной отношению времени сборки к времени обработки. В этом случае машина была бы максимально загружена и работники не простаивали бы в ожидании ее освобождения. В действительности, в силу случайного характера этих времен, оптимальное число работ­ников будет отличаться от значения, рассчитанного таким образом. Так как количество вариантов невелико, то можно воспользоваться методом их перебора, проводя эксперименты с разным числом работ­ников, начиная с одного. Таким образом, предполагаемый доход бу­дет вначале увеличиваться до некоторого момента, а когда на каком-то шаге (при большем количестве работников) доход станет меньше, чем на предыдущем шаге, нужно остановиться. Оптимальное количе­ство работников соответствует шагу с самым большим значением до­хода.

Для оценки дохода на каждом шаге при некотором фиксирован­ном количестве работников будем выполнять 10 прогонов с разными начальными множителями генераторов случайных чисел и рассчиты­вать среднее арифметическое получаемого дохода. В общем случае число прогонов надо рассчитывать с учетом требуемой точности оценки прибыли.

Добавим к модели программный текст на языке PLUS, реали­зующий вышеприведенный алгоритм поиска оптимального количест­ва работников.

EXPERIMENT Go(Parl) BEGIN

TEMPORARY CurYield,ShowString,CommandString;

NWorkers=Parl;

CurYield=GetResult();

ShowString = PolyCatenate(" Profits ",String(CurYield),". ");

ShowString - PolyCatenate(ShowString," Number of workers ",String(NWorkers),".");

CommandString = PolyCatenate("SHOW """,ShowString,.....'", "");

DoCommand(CommandString);

END;

PROCEDURE GetResultO BEGIN

TEMPORARY Sum, CurYield, Ind_i,•

Ind_i=l;

Sum=0;

WHILE (Ind_i<10)DO BEGIN

CurYield=DoTheRun(Ind_i);

Sum=Sum+CurYield;

lnd_i=Ind_i+1;

END;

RETURN (Sum/(Ind_i-1));

END;

PROCEDURE DoTheRun(Run_Number) BEGIN

DoCommand (" CLEAR OFF");

TEMPORARY CommandString;

CommandString = Catenate("RMULT ",Run_Number#3);

DoCommand(CommandString);

DoConmand (" START 1");

RETURN (FC$Machine#5-400-№Vorkers#150);

END;

EXPERIMENT Seek_Opt() BEGIN

TEMPORARY ShowString,CommandString;

TEMPORARY Prevl,Curl,Flagl;

NWorkers = 0;

Prevl=-100000;

Flagl=l;

WHILE (Flagl 'NE' 0) DO BEGIN

NWorkers=NWorkers+l;

Curl=GetResult();

IF (Curl<Prevl) THEN BEGIN

/*show results*/

ShowString = PolyCatenate(" Optimum. Profits ",String(Prevl),". ");

ShowString=PolyCatenate(ShowString," Number of workers ",String(NWorkers-1),".");

CommandString = PolyCatenate("SHOW """,ShowString,"""", "");

DoCommand(CommandString);

Flagl=0,-

END;

ELSE Prevl=Curl;

END;

END;

Переменная Flagl используется для управления циклом. Снача­ла ей присваивается значение 1, условие выхода из цикла: Flagl = 0. В переменной Prevl хранится значение дохода на предыдущем шаге. Вначале ей присваивается очень большое по модулю отрицательное значение, чтобы получаемый доход на первом шаге заведомо был больше. На каждой итерации цикла количество работников N Workers увеличивается на 1. Перед входом в цикл оно устанавливается рав­ным 0.

Переменная Curl получает значение дохода на текущем шаге. Если предыдущее значение дохода больше текущего, то выдается ре­зультат и осуществляется выход из цикла.

Для запуска эксперимента сначала нужно оттранслировать мо­дель вместе с написанным программным текстом. Для этого выпол­няем пункт меню Command/Create Simulation. Все написанные про­цедуры регистрируются в системе. Затем в меню нужно выбрать пункт Command/CONDUCT. В результате появится диалоговое окно 'Conduct Experiment' Command (рис. 9.16).

Рис. 9.16

Для запуска пользовательского эксперимента, осуществляющего поиск оптимального числа работников, нужно в поле окна дописать название эксперимента Seek_Opt(). Если же нас интересует оценка величины прибыли для конкретного числа рабочих, например, для трех, то необходимо вызвать эксперимент Go(3).

В результате выполнения эксперимента Seek_Opt() в журнале сессии появится множество записей, соответствующих выполняемым прогонам и, в конце концов, такой результат:

02/10/03 01:15:21 " Optimum. Profits 298.8888888888889. Number of workers 5."

Понятно, что при желании можно выдавать любые промежуточ­ные данные. Таким образом, оптимальное количество рабочих со­ставляет 5, а доход равен 298,89 единиц стоимости, что совпадает с оптимизирующим экспериментом (отличие в величине дохода объяс­няется разными подходами к формированию этой величины).

Подобным образом можно искать оптимум в задачах с любым количеством изменяемых параметров, нужно только вложить друг в друга циклы WHILE и перед поиском наилучшего значения целевой функции для конкретного значения параметра запоминать значение отклика для предыдущего значения этого параметра.

Пример 9.7 [10]. Рассмотрим швейное производство, в котором используются 40 собственных станков для изготовления продукции. Эти станки работают 150 ± 26 часов, после чего ломаются. Поломав­шийся станок забирается в ремонтную мастерскую, где работает не­которое число рабочих, каждый из которых может ремонтировать один станок. Ремонт осуществляется в течение 8 ± 3 часов, после чего станки снова готовы к работе. Недозагрузка производственных мощ­ностей обходится в 140 единиц стоимости в час за один станок из-за потерь, которые несет производство по недовыпуску продукции. Оп­лата одного рабочего составляет 4,75 единиц стоимости в час.

Кроме 40 собственных станков, имеющихся у предприятия, можно для подмены ломающихся арендовать аналогичные станки, Это обходится в 2,5 единицы стоимости в час за станок. Если в рабо­те уже задействовано 40 станков, то отремонтированный станок ста­новится в резерв.

Определить количество арендуемых станков и количество ра­ботников в ремонтной мастерской, при которых средние затраты на производство были бы минимальными.

Для поиска оптимума будем «разрезать» поверхность отклика плоскостями, которые соответствуют фиксированным значениям ко­личества арендуемых станков и нанятых ремонтников. При фиксиро­ванном значении одного параметра график функции затрат будет представлять собой кривую в двумерном пространстве с одним ми­нимумом (его можно найти точно так же, как в предыдущем приме­ре). Таким образом, если мы будем последовательно изменять один параметр, по которому производится разрезание поверхности, то по­лучаемые значения функции затрат при этом фиксируемом параметре будут сначала уменьшаться, а потом в какой-то момент снова пойдут на увеличение. Самое маленькое значение и будет наилучшим. Это следует из предполагаемого вида поверхности.

Программа:

MHIRED EQU 0; Количество арендуемых машин

N_WRK EQU I; Количество ремонтников

REP STORAGE 3; Начальное количество ремонтников

MANUF STORAGE 40; Количество станков

GENERATE,,,(40+M_HIRED); Общее число станков