Задача поиска минимального остова графа

Прикладные задачи теории графов

Эта задача возникает при проектировании линий электропередачи, трубопроводов, дорог и т.д., когда требуется заданные центры соединить некоторой системой каналов (связей) таким образом, чтобы любые два центра были связаны непосредственно или через другие каналы, и чтобы общая длина (стоимость) каналов связей была минимальной.

Определение. Граф называется взвешенным, если его ребрам или дугам приписаны некоторые числа (веса).

Определение. Остовным деревом или остовом графа называется связный подграф без циклов, содержащий все вершины исходного графа. Подграф содержит часть или все ребра исходного графа.

В одном графе может быть выделено много остовов (Рис.5.1.).

Рисунок 5.1 Различные остовы графа K_3.3

Задача о минимальном остове формулируется следующим образом: во взвешенном связном графе найти остов минимального веса, то есть остов, суммарный вес ребер которого является минимальным.

Рассмотрим алгоритм Краскала построения минимального остова графа. Остов строится постепенно, на каждом шаге добавляется одно ребро. В алгоритме используются два правила.

1) Первое ребро остова - ребро минимального веса в исходном графе.

2) Если в остов уже добавлено i (i<n-1)ребер, то следующее ребро е_{i +1},
есть ребро минимального веса среди ребер, которые еще не включены в остов
и не составляют циклов с уже добавленными ребрами.

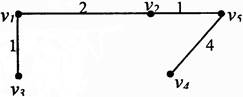Рисунок 5.2 Минимальный остов

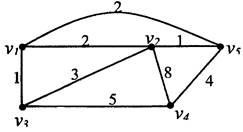
Пример 5.1. Найти минимальный остов в графе (Рис.5.2.).

Построение остова начнем с ребра (v ₁, v _j), так как оно имеет минимальный вес (можно было начать и с ребра (v₂,v₅)). Порядок присоединения ребер к остову:

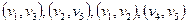
Вес остова

W=1+2+1+4=8.

Заметьте, что ребра (v ₂, v ₃), (v ₁, v ₅)не были включены в остов, хотя имели вес меньший, чем ребро (v₄,v ₅), так как они образовывали циклы с уже включенными ребрами.

Еще один пример применения рассмотренной задачи. Пусть задано множество аэродромов, и нужно определить минимальный (по сумме расстояний) набор авиарейсов, который позволил бы перелететь с любого аэродрома на любой. Решением этой задачи будет минимальный остов полного графа расстояний между аэродромами

Далее мы лишь перечислим задачи, которые возникают в теории графов и находят практическое применение. Алгоритмы их решения выходят за рамки этого курса.