Раскраска вершин графа

Раскраской вершин графа называется такое задание цветов вершин, что, если вершины соединены ребром (дугой), то они должны иметь разный цвет.

Для определения раскраски вершин графа следует учесть то, что вершины внутренне устойчивого множества не смежны, а потому их можно окрашивать в один цвет. Поскольку необходимо окрасить все вершины, то для определения числа красок приходится решить задачу минимального покрытия вершин графа внутренне устойчивыми множествами.

Составим таблицу покрытий вершин графа внутренне устойчивыми множествами (табл. 2.1). Таблица строится следующим образом.

Число строк таблицы равно мощности семейства НМВ, каждая строка обозначается именем соответствующего независимого множества вершин, число столбцов равно числу вершин графа и столбцы обозначаются именами вершин, элемент таблицы a_i,j = 1, если вершина x_j входит в множество 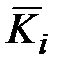, иначе a_i,j = 0 (нули можно не писать).

	x 1	x 2	x 3	x 4	x 5	x 6

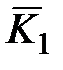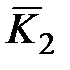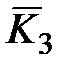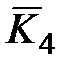Таблица 2.1

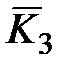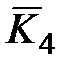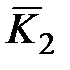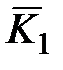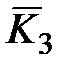Из таблицы видно, что для окраски вершины x ₁ нужна краска множества или , для окраски вершины x ₂ нужна краска множества , для вершины x ₃ – нужна краска множества или , или 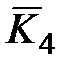и т.д.

Для окраски всех вершин нужны краски множеств, определяемых выражением

П’ = ( ) ( ) ( )( ).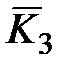

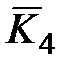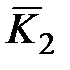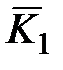
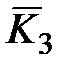
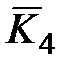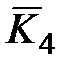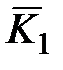
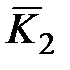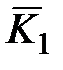
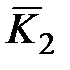
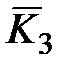После раскрытия скобок и минимизации получаем

П’= .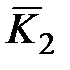

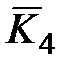Количество элементов в П’ определяет число красок, необходимых для такой раскраски вершин, при которой смежные вершины имеют разные цвета.

Минимальное число красок, достаточное для такой раскраски вершин, при которой смежные вершины имеют разные цвета, называется хроматическим числом графа и обозначается 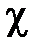(G).

Для данного примера 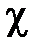(G) = 2. Вершины, входящие в 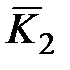, окрашиваются одной краской, например, красной (к). Вершины, входящие в 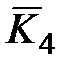, другой – белой (б). Раскраска показана на рис. 21.2.

Граф, для раскраски вершин которого достаточно двух красок, называется бихроматическим графом.

Процедура определения хроматического числа оказалась достаточно сложной. В связи с этим возникает вопрос: – А нельзя как–то по проще хотя бы оценить это число?

Ясно, что для полного графа с n вершинами 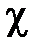(K_n) = n, так как в полном графе каждая вершина смежна со всеми другими вершинами графа. Очевидно также, что 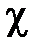(G) = 1, когда имеем нуль граф, в котором нет связей между вершинами. О хроматическом числе произвольного графа G можно только сказать, что оно лежит в пределах r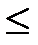 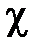(G) 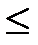n, где r – число вершин максимального полного подграфа (такой подграф называется кликой), содержащегося в графе G.

Если известны степени вершин графа, то

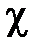(G) = maxdeg(G) + 1,

где maxdeg(G) – максимальная степень вершин графа.

Для планарных графов получена оценка 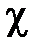(G) 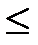5, хотя существует гипотеза о возможности раскраски любого планарного графа не более чем четырьмя красками. Однако эта гипотеза еще не доказана.

Алгоритм последовательной раскраски вершин графа

В простейшем случае последовательная раскраска вершин производится так:

1) Произвольной вершине a ₁ графа G присвоить цвет 1.

2) Если вершины a ₁,…, a_i раскрашены в 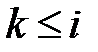цветов, то новой произвольно взятой вершине a_{i +1} присвоить цвет, не использованный при раскраске ближайших соседей.

Для некоторых классов графов последовательная раскраска минимальна. В общем случае это не так.

Более точная последовательная раскраска производится с помощью приближенного алгоритма поиска МНМВ и сводится к следующему:

1) С помощью приближенного алгоритма в заданном графе находим МНМВ. Вершины этого множества окрашиваем краской 1.

2) Удаляем из графа окрашенные вершины и инцидентные им ребра.

3) В полученном подграфе находим МНМВ и его вершины окрашиваем краской 2.

4) Удаляем из графа окрашенные вершины и инцидентные им ребра и т.д., пока не окрасим все вершины графа.

Приближенный алгоритм поиска МНМВ

В этом алгоритме используется функция предпочтения

,

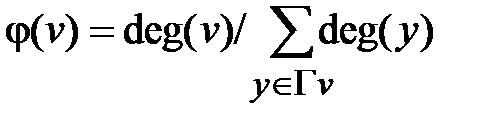где Г v – множество вершин, смежных с v.

В основу функции предпочтения положены следующие соображения:

- в МНМВ выгоднее включать вершины с малыми степеням (у них мало смежных вершин);

- вершины, смежные с включаемыми в МНМВ, должны иметь максимально возможные степени.

Алгоритм поиска МНМВ:

Имеем граф G (V, E).

Обозначим максимальное независимое множество вершин графа через S, множество вершин, смежных с вершинами из S, обозначим через Г S.

1) Положим S = 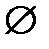. Определим для всех вершин графа значения функции предпочтения.

2) Добавляем к S вершину v, имеющую минимальное значение функции предпочтения (если таких вершин несколько, то любую из них).

3) Проверяем 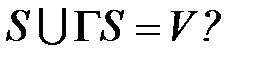Если ДА, то КОНЕЦ, иначе повторить п. 2.