Способы задания графа

Задать граф – значит описать множества его вершин и ребер, а также отношение инциндентности.

Для описания вершин и ребер достаточно их занумеровать.

Пусть 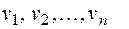вершины графа; 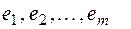ребра графа G.

Отношение инциндентности задается:

а) матрицей инциндентности 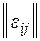размера 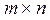(строкам соответствуют ребра, столбцам – вершины графа), в которой

для н-графа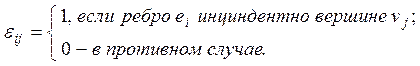

для ор-графа

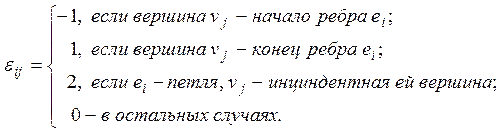
б) списком ребер графа, в котором каждая строка соответствует ребру и в ней записаны номера вершин графара, инциндентных этому ребру. Для н-графа порядок вершин в строке произволен, для ор-графа первым стоит номер вершины–начала ребра.

в) матрицей смежности 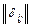размера 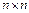, столбцам и строкам которой соответствуют вершины графа. Для н-графа 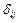равно количеству ребер, инцинентных i -й и j -й вершинам, для ор-графа 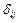равно количеству ребер с началом в i -й и концом в j -й вершине.

Вид матриц и списка ребер зависит от нумерации вершин и ребер графа. Граф считается полностью заданным, если нумерация его вершин зафиксирована.

Графы, отличающиеся только нумерацией вершин, называются изоморфными.

Перенумерация вершин и ребер графа задается соответственно строкам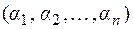и и 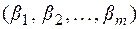новых номеров вершин и ребер, расположенных в исходном порядке.