Теорія ігор. Експліцитні та імпліцитні дерева гри

Теорія ігор – це математична дисципліна, що вивчає питання поведінки учасників конфліктних ситуацій та має на меті виробити оптимальну для кожного з учасників стратегію такої поведінки. Конфліктною при цьому називають ситуацію, коли гравці мають різні цілі (різні функції виграшу) та можуть вибирати різні засоби досягнення своїх цілей (стратегії).

Залежно від кількості гравців розрізняють ігри двох та n гравців. Ігри трьох і більше гравців менше досліджені через принципові складності й технічні можливості отримання розв’язку.

За кількістю стратегій ігри поділяють на скінченні та нескінченні. Якщо у грі всі гравці мають скінченне число можливих стратегій, то її називають скінченною. Якщо ж хоча б один із гравців має необмежену кількість можливих стратегій, то гру називають нескінченною.

За характером взаємодії ігри поділяються на безкоаліційні (гравці не мають права вступати в угоди, утворювати коаліції) та коаліційні (кооперативні), з дозволом вступати в коаліції. У кооперативних іграх коаліції визначають заздалегідь.

За характером виграшу ігри класифікують так: ігри з нульовою сумою (загальний капітал усіх гравців не змінюється, а перерозподіляється між гравцями; сума виграшів усіх гравців дорівнює нулю) та ігри з ненульовою сумою.

За виглядом функцій виграшу ігри поділяють на матричні, біматричні, безупинні, опуклі, сепарабельні, типу дуелей та ін.

Матрична гра – це скінченна гра двох гравців із нульовою сумою, у якій задано виграш першого гравця у вигляді матриці (рядок матриці відповідає номеру застосованої стратегії першого гравця, стовпчик – номеру застосованої стратегії другого гравця; на перетині рядка і стовпця матриці – виграш першого гравця, що відповідає застосованим стратегіям). Для матричних ігор доведено, що будь-яка з них має рішення і його можна легко знайти шляхом зведення гри до задачі лінійного програмування.

Біматрична гра – це скінченна гра двох гравців із ненульовою сумою, у якій виграші кожного гравця можна задати матрицями окремо для відповідного гравця (у кожній матриці рядок відповідає стратегії першого гравця, стовпчик – стратегії другого гравця, на перетині рядка і стовпця в першій матриці знаходиться виграш першого гравця, у другій матриці – виграш другого гравця). Для біматричних ігор також розроблено теорію оптимальної поведінки гравців, однак пошук розв’язків для таких ігор складніший, ніж для звичайних матричних.

Неперервною вважають гру, в якій функція виграшів кожного гравця є неперервною, незалежно від стратегій. Доведено, що ігри цього класу мають розв’язки­­­­­­­­­­­­­, ­однак практично не розроблено прийнятних методів їх знаходження.

Якщо функція виграшів є опуклою, то таку гру називають опуклою. Для таких ігор розроблено прийнятні методи рішення, суть яких у відшуканні чистої оптимальної стратегії (визначеного числа) для одного гравця та імовірностей застосування чистих оптимальних стратегій для іншого гравця. Таке завдання розв’язують порівняно легко.

Матричну гру двох гравців із нульовою сумою можна розглядати як наступну абстрактну гру двох гравців.

Перший гравець має m стратегій i = 1, 2,..., m, другий – n стратегій
j = 1, 2,..., n. Кожній парі стратегій (i, j) поставлено у відповідність число а_ij, яке виражає виграш першого гравця за рахунок другого гравця, якщо кожен з гравців візьме свою стратегію.

Кожен із гравців робить один хід: перший гравець вибирає свою i -ту стратегію ( 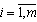), а другий – свою j-т у стратегію ( 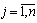), після чого перший одержує виграш а_ij за рахунок другого (якщо а_ij < 0, то це означає, що перший гравець винен другому суму | а_ij|). На цьому гру закінчують.

Кожну стратегію гравців 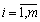, 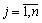часто називають чистою стра­тегією.

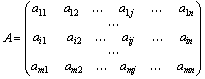
Якщо розглянути матрицю

,

то проведення кожної партії матричної гри за матрицею А зводиться до вибору першим гравцем i- го рядка, а другим – j- го стовпця й одержання першим гравцем (за рахунок другого) виграшу а_ij.

Головним у дослідженні ігор є поняття оптимальних стратегій гравців. У це поняття інтуїтивно вкладають такий зміст: стратегія гравця є оптимальною, якщо застосування цієї стратегії забезпечує йому найбіль­ший гарантований виграш за будь-яких стратегій іншого гравця. Враховуючи це, перший гравець досліджує матрицю виграшів А у такий спо­сіб: для кожного значення i ( 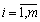) визначають мінімальне значення ви­грашу, залежно від стратегій другого гравця:

( ),

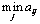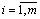тобто мінімальний виграш для першого гравця за умови, що він візьме свою i -ту чисту стратегію, далі із цих мінімальних виграшів відшукують таку стратегію i = i_про, за якої цей мінімальний виграш буде максимальним, тобто знаходять

.

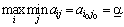Число 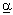, визначене за формулою (10.1), називають нижньою чистою ціною гри; воно показує, який мінімальний виграш може гарантувати собі перший гравець, застосовуючи свої чисті стратегії за будь-яких дій другого гравця.

Другий гравець за своєї оптимальної поведінки прагне завдяки своїм стратегіям максимально зменшити виграш першого гравця. Тому для другого гравця відшукують 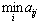, тобто визначають найбільший можливий виграш першого, за умови, що другий гравець застосує свою j -ту чисту стратегію, а далі відшукає таку свою j = j ₁ стратегію, за якої перший гравець одержить мінімальний виграш, тобто знаходить

.

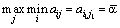Число 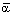, обчислене за формулою (10.2), називають чистою верхньою ціною гри; воно показує, який максимальний виграш завдяки своїм стра­тегіям може собі гарантувати перший гравець.

Інакше кажучи, застосовуючи свої чисті стратегії, перший гравець може забезпечити собі виграш не менше 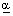, а другий гравець завдяки застосуванню своїх чистих стратегій може не допустити виграшу першого гравця більшого за .

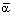Якщо в грі з матрицею А 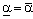, то кажуть, що така гра має сідлову точку в чистих стратегіях та чисту ціну гри .

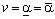Пару чистих стратегій першого і другого гравців, що утворює сідлову точку і сідловий елемент, називають розв’язком гри.

Якщо ж у грі немає сідлової точки, тоді слід знайти нижню й верхню чисті ціни цієї гри, які вказують, що перший гравець не може сподіватись на виграш, більший за верхню ціну гри, і може бути впевненим в одержанні виграшу, не меншого за нижню ціну гри. Поліпшення рішень матричних ігор варто шукати у використанні таємності застосування чистих стратегій і можливості багатократного повторення ігор у вигляді партії. Цього результату досягають шляхом застосування чистих стратегій випадково, із визначеною ймовірністю.

Змішаною стратегією гравця називають повний набір імовірностей застосування його чистих стратегій.

Таким чином, якщо перший гравець має m чистих стратегій 1, 2,..., m, то його змішана стратегія x – це набір чисел x = (x₁,..., x_m), які задо­вольняють відношенню

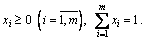
Аналогічно для другого гравця, який має n чистих стратегій, змішана стратегія y – це набір чисел:

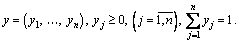
Середній виграш першого гравця у матричній грі з матрицею А виражають у вигляді математичного очікування його виграшів:

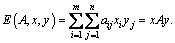
Перший гравець має на меті за рахунок зміни своїх змішаних стратегій х максимально збільшити свій середній виграш Е(А, х, y), а другий – за рахунок своїх змішаних стратегій зробити Е (А, х, y) мінімальним, тобто для розв’язання гри необхідно знайти такі х і y, за яких досягають верхньої ціни гри:

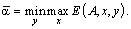
Аналогічною має бути ситуація і для другого гравця, тобто нижня ціна гри є такою:

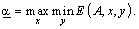
Подібно до ігор, які мають сідлові точки в чистих стратегіях, дамо визначення: оптимальними змішаними стратегіями першого і другого гравців називають такі набори х ^о, у ^о відповідно, які задовольняють рівності

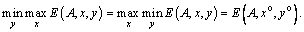
Величину Е (А, х ^о, у ^о) називають ціною гри і позначають через v.

Оптимальні змішані стратегії та ціну гри називають розв’язком матричної гри

Теорема (про мінімакс). Для матричної гри з будь-якою матрицею А величини 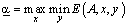і 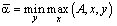існують і є рівними.

Вaжливою частиною більшості ігрових програм є процедура аналізу «дерева логічних можливостей».

Існує два типи дерев: дерева гри і дерева цілей. Гілки в дереві гри задають можливі ходи, ходи у відповідь і т. д. Дерево цілі показує, що деякої початкової цілі можна досягти, коли буде досягнуто певних підці­лей; у свою чергу аналогічно перевіряють досягнення підцілей. Оскільки де­рева мають тенденцію сильно розростатись, виникає потреба ефективного виділення істотних частин дерева. Дерево гри може бути експліцитним
та імпліцитним. Експліцитне дерево гри задають у явному вигляді, імплі­цитне ж дерево задають виділенням початкової позиції і правил формування дерева.

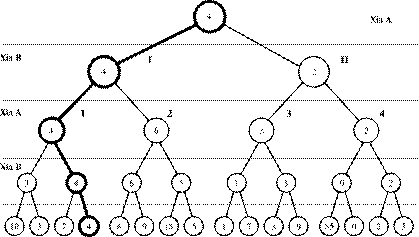
Корінь цього дерева збігається з початковою позицією. Кожен вузол цього дерева характеризується номером гравця, що має робити хід. Дуги відповідають ходам, тобто, якщо в позиції 1 можливий хід, який переводить позицію 1 в позицію 2, то з позиції 1 до позиції 2 йде орієнтована дуга, яка відповідає цьому ходу. Право вибору ходу в позиції 2 належить, звичайно, уже іншому гравцеві. Кожен вузол дерева корисно характеризувати також його рівнем, тобто відстанню від кореня. Якщо на k -му рівні право вибору ходу належить одному з гравців, то на (k + 1)-му рівнівоно переходить до його суперника.

Нехай грають два гравці – А і В. Для визначеності вважатимемо, що право вибору ходу в початковій позиції належить гравцеві А. Функція виграшу збігається з функцією виграшу цього гравця, тобто гравець А аналізує дерево гри зі свого погляду та прагне максимізувати виграш. Вершини, в яких право ходу належить гравцеві А, прийнято називати
α-вершинами; вершини ж, у яких право ходу належить його суперникові, називають β-вершинами.

Для будь-якої гри, що завершується за скінченну кількість ходів, є теоретично можливим побудувати повне дерево гри, що охоплює всі можливі позиції. Почнемо аналіз дерева з завершальних позицій (листків дерева). Розглянемо довільні завершальні позиції, які мають одного бать­ка. Нехай для визначеності це α-вершини. Кожна завершальна позиція має оцінку, що збігається з функцією виграшу та є результатом гри. Ясно, що гравець В, якому належить право вибору ходу у батьків­ській вершині, вибере хід, що мінімізує цю оцінку (мінімізує його програш). Ця мінімаль­на оцінка передається даній вершині знизу.

Нехай всі наступники довільної β-вершини уже проаналізовані та кож­ному передано знизу певну оцінку. Загальне правило можна сформулювати у такий спосіб: з β -вершини має бути зроблений хід, що веде до позиції-наступника з найменшою оцінкою.

За допомогою аналогічних міркувань можна встановити правило, згід­­но з яким повинен вибирати ходи гравець А: з α -вершини має бути зроблений хід, що веде до позиції-наступника з найбільшою оцінкою.

Такий аналіз можна зробити для будь-якої позиції, включаючи почат­кову. Ця процедура носить назву мінімаксної процедури.